ISSN: 2322-0066
ISSN: 2322-0066
Samuel Bonaya Buya*
Mathematics/Physics teacher at Ngao girls, Secondary School, Kenya
Received date: 13/05/2017; Accepted date: 05/10/2017; Published date: 06/10/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
I present a method of solving the general quintic equation by factorizing into auxiliary quadratic and cubic equations. The aim of this research is to contribute further to the knowledge of quintic equations. The quest for a formula for the quintic equation has preoccupied mathematicians for many centuries.
The monic general equation has six parameters. The objectives of this presentation is to, one, seek a factorized form of the general quintic equation with two exogenous and four indigenous parameters, two, to express the two exogenous parameters of factorization as a function of the original parameters of the general quintic equation.
In the process of factorization two solvable simultaneous polynomial equations containing two exogenous and four original parameters are formed. Each of the exogenous parameters is related to the coefficients of the general quintic equation before proceeding to solve the auxiliary quadratic and cubic factors.
The success in obtaining a general solution by the proposed method implies that the Tschirnhausen transformation is not needed in the search for radical solution of higher degree general polynomial equations.
As a way forward factorized form for solution of the general sextic and septic equations will be presented to pave way for their algebraic solution.
Radical or algebraic solution of the general quintic equation; Algebraic solution of the general sextic and septic equations
The objective of this paper is to add further to the research into the solution quintic of equations that has preoccupied mathematicians for centuries. The topic under investigation is very important in algebra and has applications in computer science in general. Investigation of algebraic solution of higher degree polynomials is prominent problem in mathematics. An extra mile will be taken to obtain the algebraic solution of the general quintic equation, as a departure from the original attempt of obtaining the solution of the trinomial quintic. That is, a method will be sought of solving the general quintic equation without recourse to the Tschirnhausen transformation. The reason for adopting this line of pursuit is to establish a basis upon which algebraic solution of higher degree general polynomials can be found [12].
The presumption of this paper is that the quadratic equation solution method and solution methods of Ferrari and Cardano and Lodvico Ferrari are sufficient in the pursuit of radical solution of general higher degree algebraic equations. On the basis of this assumption a factorization method of solution will be sought for in solving the quintic equation. The Bring approach in the search of solution of the quintic was through a tedious transformation that eliminates three intermediate parameters of the general quintic equation.
The approach that will be employed in this research is a factorization in which two unknown parameters are introduced and related to the original parameters of original unfactorized quintic equation. The other three parameters will be original parameters of the quintic equation. The method employed should be able to be extended to higher degree general polynomial equations.
For three centuries before the nineteenth centuries mathematicians attempted to obtain the general algebraic solution of polynomial equations of degree five and above without success. The effort to solving these higher degree equations culminated to the Abel-Ruffini theorem. Simply stated Abel-Ruffini theorem is an attempt to answer why there is no algebraic formula in terms of coefficients for the roots of polynomial equations of degree five and above.
Galois Theory only provided a means for solving some specific forms of higher degree polynomial equations but failed to come with general formula.
Back in the sixteenth century Francois Viète, a French mathematician, set into course the path of solving higher degree polynomial equations by relating its coefficients to the roots via elementary symmetric equations. Louis Lagrange introduced Resolvents and they were systematically used by Galois as a tool for seeking specific solution of higher degree polynomials. The Caylev Resolvent is a Resolvent for the maximal resolvable Galois group in degree five.
In the seventeenth century (1666) Sir Isaac Newton found the Newton identities, though they were found earlier by Albert Girard in 1629. Thus the Newton identities are also known as Newton-Girard formulae. Newton’s identities relate the k-th power of all roots of a polynomial to its coefficients. Newton’s identities have many applications in Galois and group theory. Newton-Girard and Viète formulae are basically formulae relating the coefficients of a polynomial to its roots.
Formulae connecting roots and coefficients of polynomials have been used to seek algebraic solutions of polynomial equations.
Statement of the Problem
Could there be an effective factorization technique that can be used to solve higher degree polynomial?
If such a technique is possible what is the form should it take for easy solution of higher degree polynomial equations?
In adopting a factorization as a method of solving higher degree polynomial equations, is it possible to reduce the newly introduced parameters to two to complement the original parameters of the polynomial?
Is it possible to come up with a factorization common algorithm that can be used to solve higher degree general polynomial equations?
Is the Galois Theory approach the most effective and complete approach of seeking for solution of higher degree polynomial equations?
General Objective
The general objective of this research is to present a method in which the general quintic equation can be solved and to establish a factorization algorithm that can be used to solve higher degree general algebraic equations.
Specific Objectives
To establish the most effective factorization approach that can be used to solve quintic and higher degree polynomial equations
To establish a factorization technique that involves solving two simultaneous equations
To find the algebraic solution of the general quintic equation.
To establish the basis of algebraic solution of polynomial equations of degree greater than five
Research Questions
Is Galois Theory a complete theory? Could there be missing links and connections in Galois Theory? During the second decade of this century it was shown that algebraic solutions that at least algebraic solutions of fifth degree do exist, [3,4,6].
Furthermore Camille Jordan showed that any algebraic equation may be solved using modular functions. One such formula was achieved by Carl Johanness Thomae in 1870. The formula was achieved a Tschirnhaus transformation. The real practical application of the formula however is very difficult because of the complexity of the relevant hyperelliptic integrals and higher genus theta functions. These approaches, however, do not provide algebraic solutions but they have at least shown that other approaches do exist for solving higher degree polynomial equations.
Justification
Algebra is essential in the study of mathematics, the sciences and engineering. Algebra merges in all areas of mathematics and has many applications in geometry, computer programming and so on. Algebra plays an important role in physics etc.
Scope
The paper is simple enough and is within the mathematical reach of a student who has done mathematics at high school.
The paper is also of great value furthering the understanding of methods of solving algebraic equations of higher degree. The paper is also of great value in undergraduate mathematics, e.g. in matrices where knowledge of methods of solving polynomial equations are highly needed.
The objective of this paper is to add to the research on algebraic solution of higher degree polynomial equation. Many researchers of mathematics and the physical sciences have been occupied on the subject for centuries. Indeed literature indicates that polynomial equations have been investigated for more than four thousand years. The elegant and practical notation that we use today in determining the roots of polynomial equations developed in the beginning of the fifteenth century. Cubic and quartic polynomial equations were comprehensively solved in the sixteenth century. Three centuries later the quintic equation could not be solved. In 1824 Niel’s Abel published his impossibility theorem as an answer to the persistent algebraic insolvability of general quintic equations and higher degree polynomials equations. Earlier, in 1798, Carl Friedrich Gauss in section 359 of his book entitled Disquisitiones Arithmetica conjectured (published in 1801) about the impossibility of radical solution of the quintic equation. Abel’s impossibility theorem was almost proved by Paolo Ruffini in 1799. Abel’s theorem did not sufficiently did not provide necessary and sufficient conditions on which quintic specific quintic (or higher) equation were solvable in radicals. It was Galois Theory which completed that which lacked in Abel’s theorem. Galois Theory (Published in 1846) suggested that the impossibility theorem was strictly stronger than the result of Abel-Ruffini theorem. As Ian Stewart wrote “for all that Abel's methods could prove, every particular quintic equation might be soluble, with a special formula for each equation.”Galois Theory dampened any hope of obtaining radical solution of algebraic equations of degrees greater than four.
Bring radicals were introduced by Erland Bring and roots of the Bring-Jerrard quintic equation may be expressed in terms of Bring radicals. Many other characterizations of the Bring radical were developed by other mathematicians.
Charles Hermite published the first known solution of the general quintic equation in terms of elliptic modular functions in 1858. Some others like Francesco Brioschi and Leopold Kronecker derived similar results around the same time. Camille Jordan showed that any polynomial equation may be solved by use of modular functions. Carl Johannes Thomae achieved such a solution in 1870. In 2011 Edward Thabo Motlotle contributed to the first algebraic solution of the Bring-Jerrard quintic equation. Buya S.B. made further contributions to algebraic solution of higher degree polynomial equations between 2013 and 2017
Theoretical Review/Conceptual Framework
From the theoretical and conceptual viewpoint, polynomial equations are built out of sums and products. Each of coefficients of the polynomial codes within it the sum and product of roots in a characteristic way depending on the degree of the term it is associated with. The coefficient attached to the degree zero term is solely built from the roots of the polynomial equation.
Methods of solving polynomial equations algebraically involve extracting the roots from the coefficients through a finite process of multiplication addition and subtraction. It has been shown that a coefficient of a polynomial can be related to a general root L and other coefficients. This means a parameterization can be adopted in which one of the parameters forming a coefficient attached to a given term of a given degree is also a root. This means also that the polynomial can be linearly factorized based on this relationship. This concept is not made use of in contemporary algebra and in Galois Theory.
The formulae of quadratic, cubic and quartic equations have basically similar structure.
Methods of solving cubic equation basically involve reducing it to a depressed cubic and making substitutions for the unknown that convert it degree six equation of quadratic form. Methods of the solving quartic equation basically involve factorizing to two quadratic factors and correlating the coefficients of the factors to the coefficients of the original quartic equation. The next step is to solve the auxiliary quadratic equations with the correlated coefficients. In both cases there is a step involving a polynomial equation with quadratic a form. The resolvent approach initiated by Lagrange and extended by Galois was successful in the quadratic, cubic and quartic equations. It involves relating the roots of the polynomial equation to the coefficients via the elementary symmetric polynomials resulting from expansion of the linear factorized form of the polynomial. In solution of polynomial equations of degree greater than five the method hits a snag and reaches a dead end (even with the aid of Newton’s identity). The inability of Galois resolvent (and modern field and group approach) to obtain general solution of higher degree polynomial does not mean their insolvability. It only reflects the limitations of the approach and tool used. Other approaches have been shown to work effectively [2-8].
Strengths of Galois Theory
The resolvent approach and Galois Theory have great success in obtaining algebraic solution of polynomial equations of degree less than for.
It provides remedial and algebraic solutions of some specific forms of higher degree polynomial equations.
Weaknesses
It does not provide for methods of obtaining general radical solution general polynomial equations of degrees greater than four. The Galois resolvent approach becomes complicated to levels of indeterminacy in endeavors for seeking general solution of higher degree general polynomial equations. Galois Theory is too abstract and even misleading by purporting algebraic insolubility of higher degree general polynomial equation. The Galois and Lagrange Resolvents complicate the effort to obtain formulae for general polynomial equations of degree five and above. Galois Theory does not provide for other possible connections between the coefficients of a polynomial and coefficients of auxiliary polynomial equations in cases of non-linear factorization. It heavily relies on solving the elementary symmetric equations via Galois resolvent and Newton’s sum formula. Galois Theory permits outdated concepts of irreducible quintics. As long coefficients of auxiliary factors can be connected to those of the general polynomial that cannot be the case. Existence of irreducible quintics would actually means insolvability in the general sense. In reality general quintic equation are algebraically solvable [5,9].
Galois Theory does not consider possible factorized forms that can yield general algebraic solutions. It has does not accommodate other possible algebraic correlations between roots and coefficients that can yield the required result. In any polynomial there is for example connection between a general root L and its coefficients which forms the basis of its linear factorization [10,12]. In any polynomial there exists a correlation between a given coefficient, a general root L and other coefficients. When such connections are established we get an effective tool that can be used to obtain an algebraic solution [13].
Opportunities
Galois Theory needs to incorporate solvable factorized form for higher degree polynomials to enable correlation of the coefficients of the auxiliary polynomial equations to those of the polynomial whose solution is being sought. Correlating the coefficients of the auxiliary equation to those of the main polynomial is an indirect way of solving the elementary symmetric equations of the main polynomial [14,15].
Threat
If Galois Theory fails to incorporate these opportunities then there is a threat that it will be obsolete [16-18].
A conceptual framework exists by which higher degree polynomial equations can exist.
Method
The general quintic equation is given by:
The general quintic equation takes the form 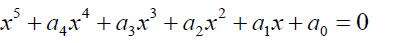 (1)
(1)
The trinomial or Bring-Jerrard form of the above equation is given by 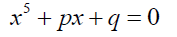 (2)
(2)
A factorized form of the general quintic equation can take the form 3 below:
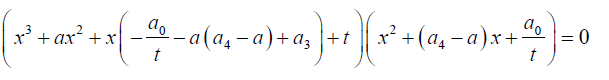 (3)
(3)
Expanding equation 3:
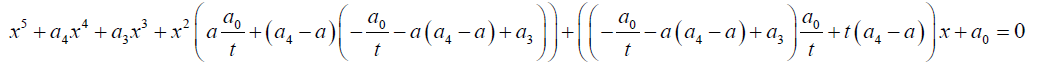 (4)
(4)
Equating coefficients:
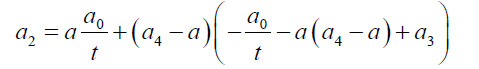 (5)
(5)
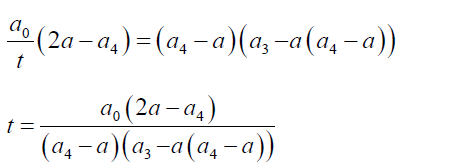 (6)
(6)
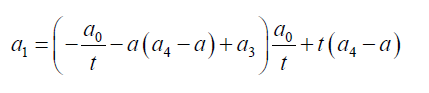 (7)
(7)
Substituting 7 into 6:
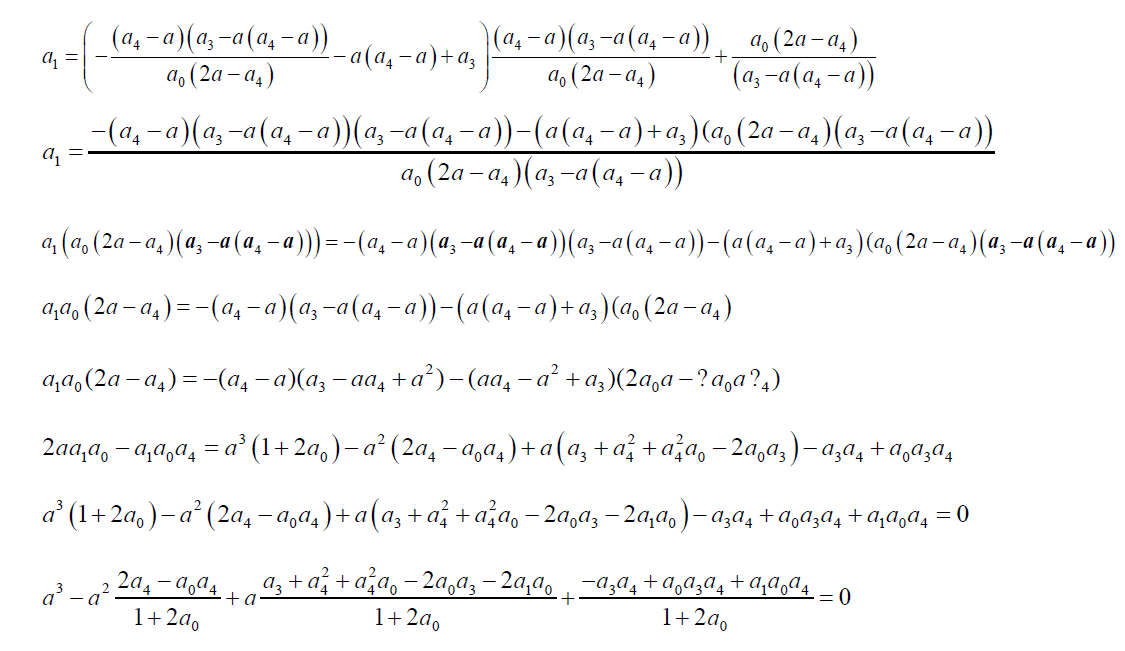 (8)
(8)
Take 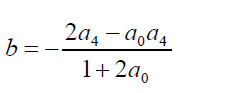 (9)
(9)
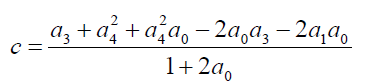 (10)
(10)
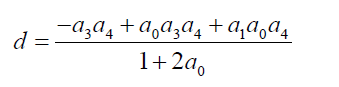 (11)
(11)
If 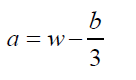 (12)
(12)
Then
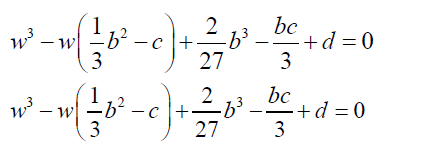 (13)
(13)
The Cardano solution of one of the roots of 8 is given by:
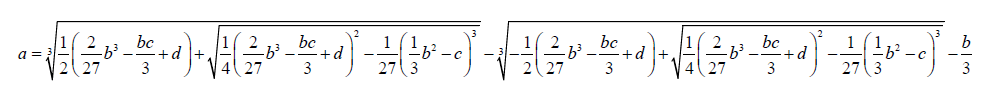 (14)
(14)
We have succeeded in relating the exogenous parameters of the auxiliary cubic and quadratic equation. We can now go on to get the Cubic and quadratic solutions of the general quadratic equation.
The auxiliary cubic equation of the general quintic equation is given by:
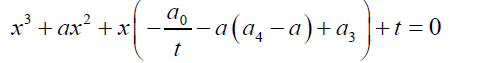 (15)
(15)
If we take 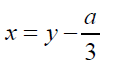 (16)
(16)
Then:
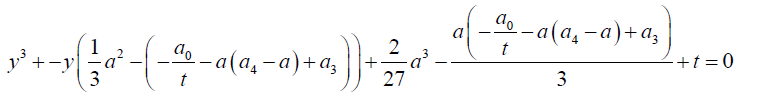 (17)
(17)
The Cardano Solution of equation 15 is given by:
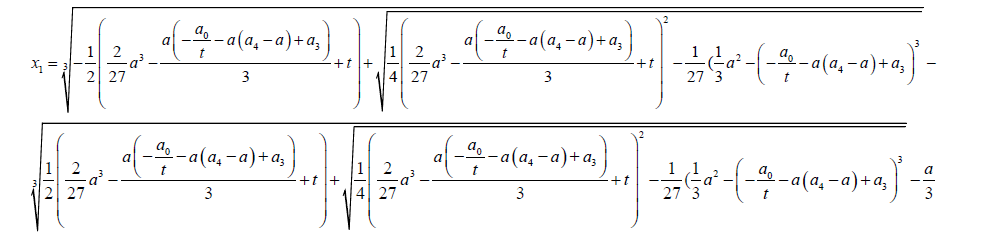 (18)
(18)
We can get the remaining roots of the auxiliary cubic equation 15 by considering the factorization:
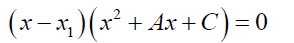 (19)
(19)
The expansion of 19 gives:
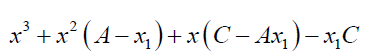 (20)
(20)
Equating coefficients:
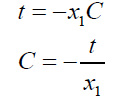 (21)
(21)
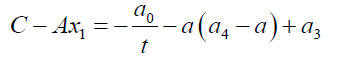 (22)
(22)
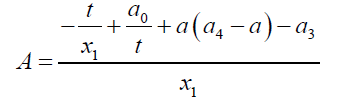 (23)
(23)
Solving the remaining roots of the auxiliary cubic equation involves solving the cubic equation 24 below:
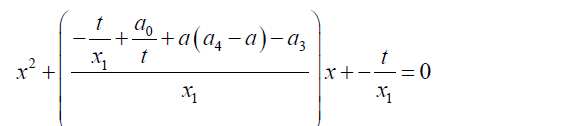 (24)
(24)
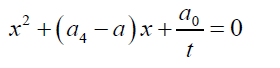 (25)
(25)
The auxiliary quadratic equation is given by:
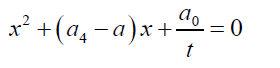 (26)
(26)
The remaining roots of the general quartic equation are given by:
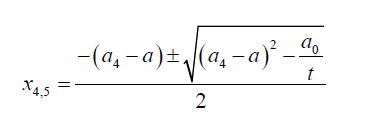 (27)
(27)
Factorized forms for solving Sextic and quintic equations
The general sextic equation takes the form
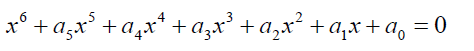 (28)
(28)
A factorized form for solving sextic equations based on the above reasoning is given by:
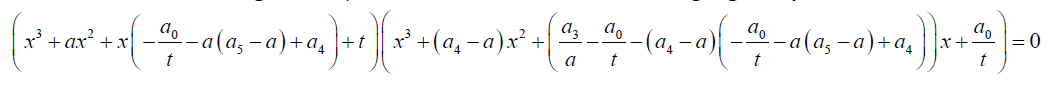 (29)
(29)
The expansion of equation 29 is given by:
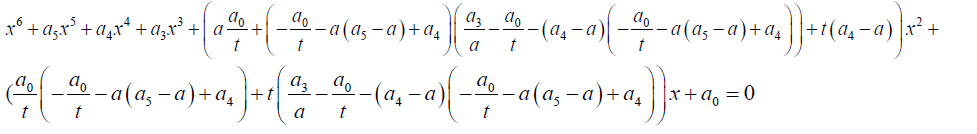 (30)
(30)
Equating coefficients
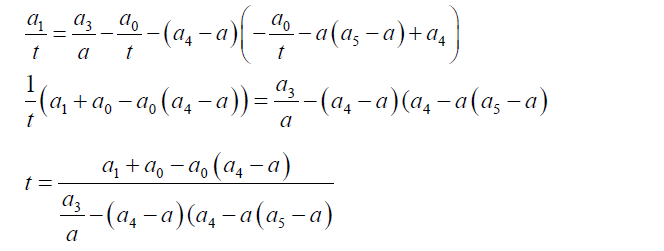 (31)
(31)
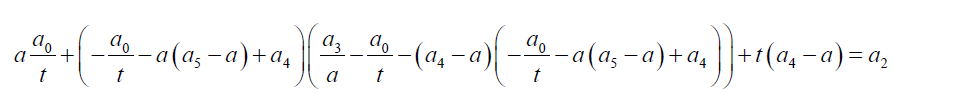 (32)
(32)
Substituting 31 into 32 we obtain the equation 32.
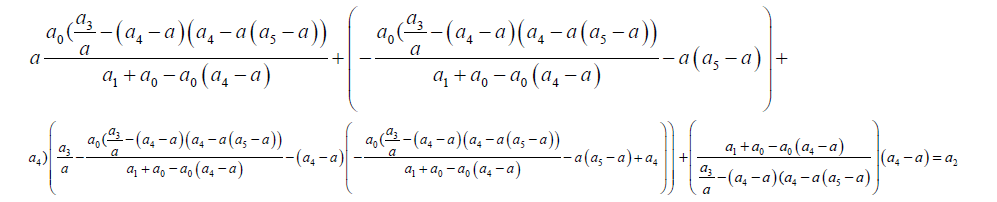 (33)
(33)
To obtain the general solution of the sextic equation solve equation 6 followed by solving the auxiliary cubic equations using the Cardano formula. In attempting to solve equation above it should be that a general quintic equation in α is algebraically solvable using the procedures outlined in this paper. In this paper I will not attempt to seek a solution for equation 33.
The general septic equation takes the form
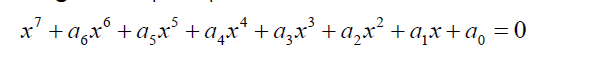 (34)
(34)
A factorized form of the general sextic equation is given by:
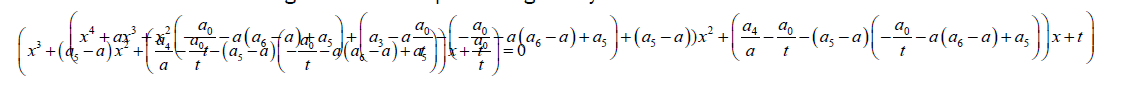 (35)
(35)
Again the algebraic solution of the general septic involves first obtaining the algebraic solution of parameters a and t.
A solution of the general quintic equation has been arrived at and without a Tschirnhaus transformation. An algorithm has been achieved by which higher degree general polynomial equations can be solved algebraically.Galois Theory requires a rewrit ng. Abel-Ruffini impossibility theorem requires some re-examination. I recommend that further research into algebraic solution of general algebraic equations using the algorithm provided in this paper.