The New Calculus

Keywords

Tangent lines; Derivatives; Asymptotic equations; Logical derivative

DESCRIPTION

The basic problem of differential calculus is the problem of tangent lines and calculating the slope of the tangent line to the graph at a given point P and the less seemingly important problem of defining the vertical asymptote line and its derivative. L’hopitals indeterminate forms and extracting real value of asymptotic equations are easily solved by applying “the logical derivative”. These are new derivatives developed using a method of direct proportions. By reversing the decrement, all derivatives derived are of the same dimension as their functions.

Derivatives of increasing functions are similar in nature to increasing functions; and decreasing functions generate derivatives of decreasing nature-logical, but most of all sensible; It is now also possible to compute tangent line equations and also of those with vertical asymptotes [1].

Newton’s power rule based on lesser reasoning than required is now extended; summative expressed as a sum of linear terms; and the difference quotient is logically analyzed linear and directly proportional; flat tangent line equations of all functions are computed with the “logical derivative”.

Tangent lines for all points on a circle, ellipse, hyperbolas are derived viz. the method presented in my work. A proof for the interdependency between minimum and maximum points for all curves is employed and readily available should you ask for it and require publishing. Newton’s hypothesis of “instantaneous rate of change” remains the solid scaffold on which all calculus is based. The motivation and obsession for seeking further precision in Newton’s voluminous and monumental work [2-6].

Newton’s calculus revised

Logical derivatives

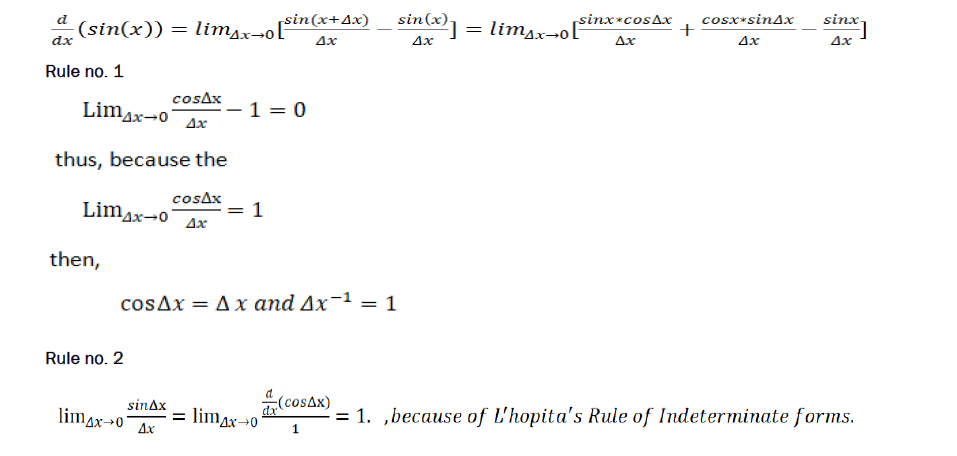
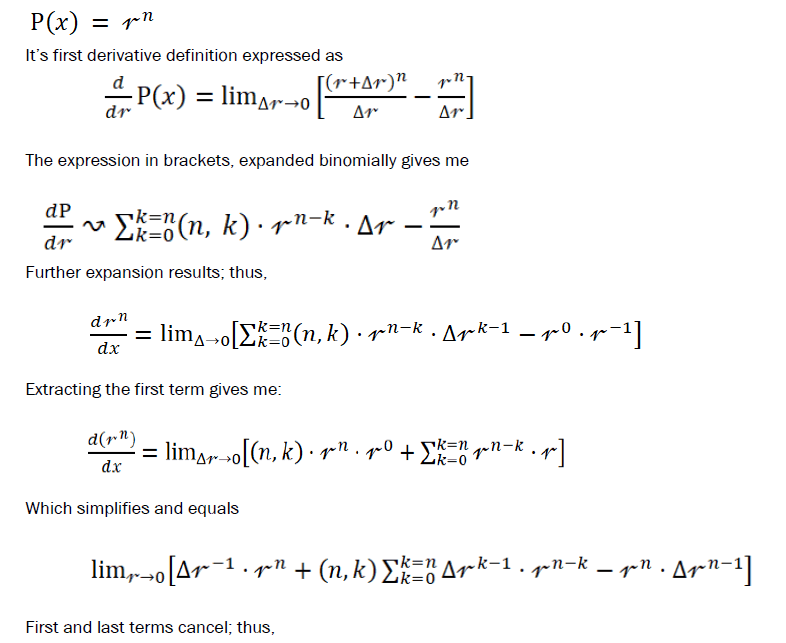
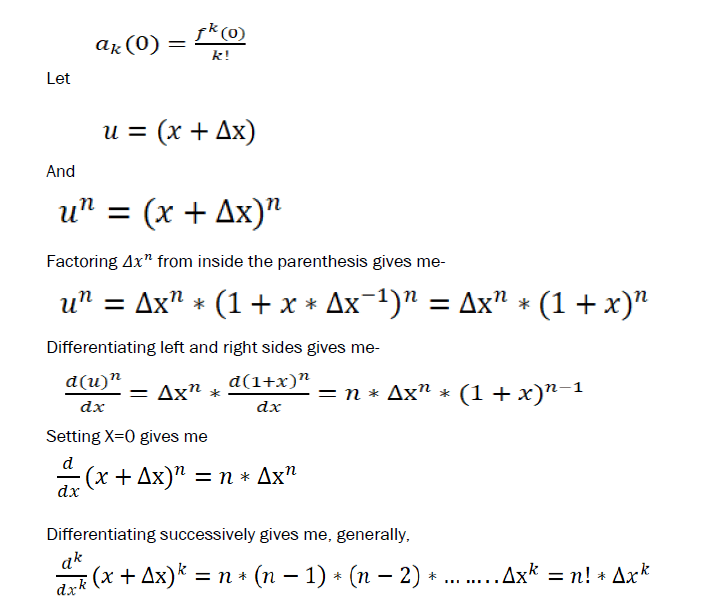
Example:

Figure 1: The tangent lines to the graph at x=0 and x=4.

To find the tangent line at the origin of the graph I square both sides to get:

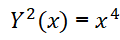
Differentiating both sides, implicitly for n=2; at the left side between 0 ≤ k ≤ 2
The derivative consists of 4 terms; thus,

Figure 2: THE instantaneous point of the curve.

Figure 3: The tangent line at the origin.

Figure 4: Tangent line equation at x=1.

Figure 5: The vertical asymptote lines of Newton’s circle.

Figure 6: Horizontal tangent lines.

Figure 7: The horizontal tangent lines.

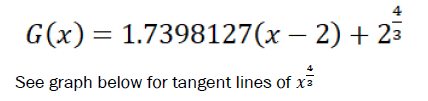
Method of solution of n-degree polynomial
Step 1. Square both sides.
Step 2. Implicitly differentiate the left and right side of the equation.
Step 3. Set the left side or the dependent side of the function equal to zero.
Step 4. Determine the solutions of the 2n-1 degree polynomial or the zeroes of the right side of the function of
-x.
Step 5. Step 4 determines the minimums and maximums of the n-degree polynomial.
Step 6. Determine the logical derivative of the n-degree function.
Step 7. Plot tangent lines of the minimums and maximums given I step 5.

References

1. Cusack PTE, et al. The ether as teflon. Mod App Matrl Sci. 2020;2:56.

   [Crossref] [Google Scholar]

2. Cusack PTE, et al. The ether and the electrical universe. Mod App Matrl Sci. 2020;2:23-27.

   [Crossref] [Google Scholar] [PubMed]

3. Cusack PTE, et al. Crystal in the ether VII. J Phy Opt Sci. 2020;5:74-76.

   [Crossref] [Google Scholar]

4. Hofstein A, et al. The role of the laboratory in science teaching: Neglected aspects of research. Rev Edu Res. 1982;52:201-217.

   [Crossref] [Google Scholar]

5. Carter L. Globalisation and science education: Rethinking science education reforms. J Res Sci Teach. 2005;42:561-580.

   [Crossref] [Google Scholar]

6. Cobern William W. et al. Defining “science” in a multicultural world: Implications for science education. Sci Edu. 2001;85:50-67.

   [Crossref] [Google Scholar]