Three Nucleon Force in α- 4He Elastic Scattering at Medium Energy

Abstract

In the framework of optical limit approximation with inclusion of the threenucleon force effect we obtained a reasonable agreement with the experimental data of α^-4He elastic scattering differential cross section at the momenta 4.32 GeV/c, 5.07 GeV/c and 7 GeV/c. We show that the three-nucleon force effect cannot be neglected in nucleus-nucleus scattering.

Keywords

Nucleus-nucleus scattering, Elastic scattering, Particle collision.

Introduction

To study nucleus-nucleus scattering at medium and high energies, a generalization of Glauber multiple scattering approximation [1], to nucleus-nucleus collision was obtained and applied to deuteron-deuteron collision at incident momentum in the range 1.5-4.4 GeV/c [2]. Czyz and Maximon presented a model for nucleon-nucleus and nucleus-nucleus scattering in the framework of Glauber model [3]. They used their approach with inclusion of Coulomb effect to study α^-4He elastic scattering at laboratory momentum 7.33 GeV/c [4]. The Coulomb effect was observed at the minima. Franco and Varma used the expansion of optical phase shift function of nucleus-nucleus collision to study light nuclei scattering at 0.87 GeV/nucleon and 2.1 GeV/ nucleon [5]. In the same approach Varma showed that the agreement with experimental data of α^-4He elastic scattering at α incident momenta 4.32 GeV/c and 5.05 GeV/c has improved considerably when short-range dynamical correlations in nuclei were introduced [5,6].

The rigid projectile model [7] and Czyz-Maximon model [3] were used to interpret the measurement results of Satta et al [8] for α^-4He elastic scattering differential cross section at α incident momentum 7 GeV/c. The rigid projectile model could not describe the experimental data, while Czyz-Maximon model can be used with further theoretical improvement.

Using multiple scattering Glauber theory, Franco and Yin [9,10] introduced nucleonnucleon amplitude phase variation to investigate α- 2He, 3He and 4He elastic scattering at medium energies, 4.32 GeV/c, 5.07 GeV/c of [11] and 7 GeV/c of Satta et al. [8]. The inclusion of the phase variation leads to a clear improvement in agreement with the experimental data.

Usually, the Single-Gaussian wave function of 4He was used in many works to calculate α^-4He cross sections. However, Usmani et al, in the framework of Glauber multiple scattering model, show that the results with Double-Gaussian model wave function of 4He at α- particle momenta 4.32 GeV/c, 5.07 GeV/c, and 7.0 GeV/c, were closer to experimental data of α^-4He cross sections as compared to the results of Single-Gaussian model. Also, in the same multiple scattering theory, the same authors [12], used two correlated variational wave functions as given by two different potentials to calculate α^-4He elastic scattering differential cross section at 4.32 GeV/c [13]. These two wave functions gave fairly acceptable results.

Despite, the satisfactory results of the previous works, there is still a place for other additives that may improve the obtained results and take into account some effects that have not been taken before.

In this article we will use the optical limit approximation of Glauber theory to calculate α^-4He elastic scattering differential cross section at the incident momenta 4.32 GeV/c, 5.07 GeV/c [11] and 7 GeV/c [8] for α particle. The zero spin and isospin of the α-particle simplify the cross-section calculations of α^-4He elastic scattering. We know that the α-particle is a composite particle pointing to 4Henucleus. Therefore, the Glauber formalism of α^-4He is the same as 4He-4He Hescattering formalism.

Many suggestions were used to obtain a good fit with the α^-4He elastic scattering data, see [4-7,9,10,12,13]. For example, a good agreement with the experimental data of [11] at 4.32 GeV/c, 5.07 GeV/c and of [8] at 7 GeV/c was obtained by the inclusion of the phase variation of nucleon-nucleon amplitude [9,10]. However, the phase variation has different meaning from different points of view. In [9,10] the authors considered the phase variation as a proper property of the nucleon-nucleon amplitude. While in [14] the authors considered the phase variation as a result of collision, meaning that the amplitude of the first collision has no phase variation, but, the amplitude of the second collision has a phase variation due to the first collision and so on. At the same time, the phase variation effect can be clearly observed at minima, as well as the Coulomb effect, and at each minimum we need a certain value for the phase variation parameter to obtain an agreement with the data. This value is different at the other minimum. Therefore, we try to use the three-nucleon force correction to obtain reasonable description of the data. We can consider that the three-nucleon force represents, in the framework of the meson theory, a clear physics as a result of 2π exchange between three nucleons.

The used approach to introduce the three-nucleon force effect was suggested at first in [15] for particle-nucleus scattering at medium and high energies and applied on hadrondeuteron elastic scattering in the framework of multiple scattering theory of Glauber. The same approach was formulated for hadron-deuteron elastic scattering in optical limit approximation of Glauber [16]. This approach was applied for p-3He and p-4He to study the three-nucleon force effects [17,18]. Also, the authors in [19,20] generalized this approach, in the framework of optical limit approximation, to study three-quark force in proton-proton elastic scattering as composite particles of three quarks constituents at ISR and LHC energies. In all these works the importance of the three-nucleon or three-quark forces was proven. Therefore, we try to use the generalization of [19,20] to study three-nucleon force effect in nucleusnucleus elastic scattering in the framework of optical limit approximation. It should be remembered that this generalization can also be used in the framework of Glauber multiple scattering theory.

The Model

In the optical limit approximation, the scattering amplitude F(q) of nucleus-nucleus elastic scattering is given by [1,16,19]

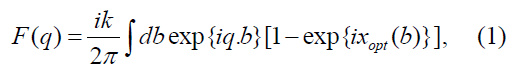
where q is the momentum transfer vector, b is the two- dimensional impact vector between the mass centers of the two nuclei and k is the momentum of incident nucleus. The total optical limit phase shift x_opt(b), including three-nucleon force [16, 19], is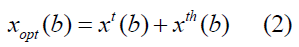

where, x^t(b) is the two-nucleon force phase shift, x^th(b) is the three-nucleon force correction. From the additivity property of the phase shift for the two-nucleon and three-nucleon force phase shifts, we have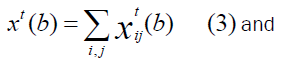

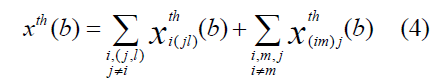
where 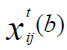is the two-nucleon force phase shift, 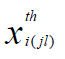is the three-nucleon force correction where the nucleon j and nucleon l are target nucleons and 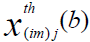is the three-nucleon force correction where nucleon i and nucleon m are incident nucleons. In this approach, i(jl) means that the incident nucleon i collides with the target nucleon j and, at the same time, the target nucleon j interacts with another target nucleon l. Also, (im)j means that the incident nucleon i collides with the target nucleon j and, at the same time, the incident nucleon i interacts with another nucleon m in the incident nucleus. In terms of twonucleon and three-nucleon force profile functions 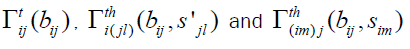the phase shifts 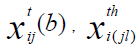and 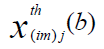are [1,16, 19].

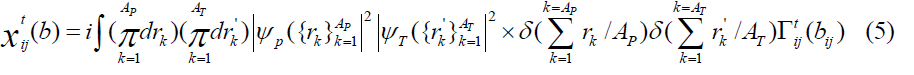
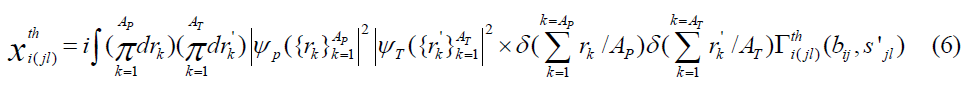
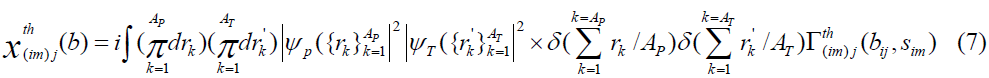
where 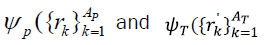are the ground state wave functions of the incident and target nucleus, respectively, 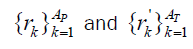are the position vectors of nucleons inside the incident and target nuclei, respectively. The Dirac δ function expresses a constraint on the 5 nucleus center of mass. The vectors 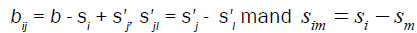where s_i and s_j are the projections of the position vectors r_i and r_j on the impact plane.

The two-nucleon force profile function 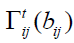and the three-nucleon force profile functions 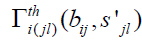and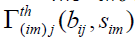 are taken as follows [16,19].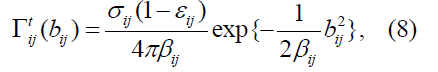

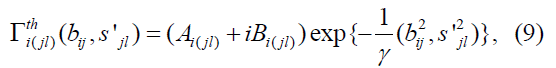
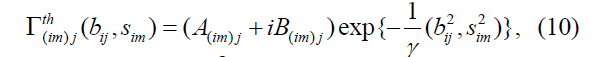
where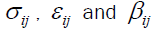 are total cross section of nucleon-nucleon collision, the ratio of real part to imaginary part of the amplitude in the forward direction and the slope parameter, respectively. The quantities 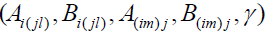are the three-nucleon force parameters.

For α-⁴He scattering the mass numbers AP=AT=4 and 4He wave function is taken in the Gaussian form.

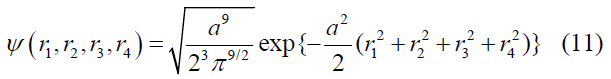
The constant α is related to the root mean square radius 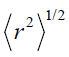of ⁴He nucleus by the relation 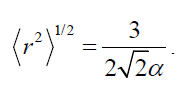For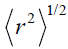 we take the experimental value of point nucleon density radius, 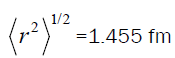[21]. This value was obtained, also, by using different nucleon-nucleon potentials, CD-Bonn 2000 potential [21], Nijmegen and Reid Soft Core potentials [22]. Thus, we get α=0.729 fm^-1.

Consider the coordinate transformations

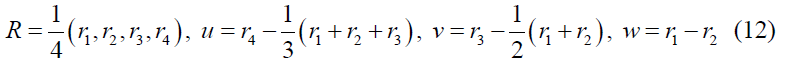
Thus, the inverse transformations are

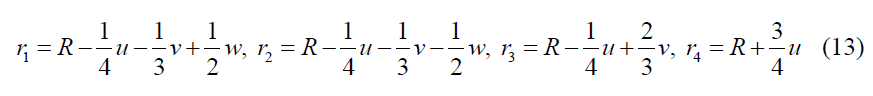
The wave function Ψ in the new coordinates takes the form

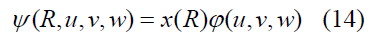
where 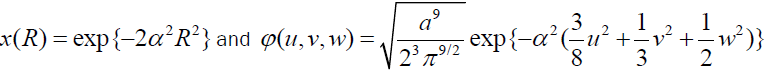represent the center of mass motion and relative motion in the nucleus, respectively. Using the new coordinates and integrating over R and R’ the phase shiftsHe elastic scattering take the forms.

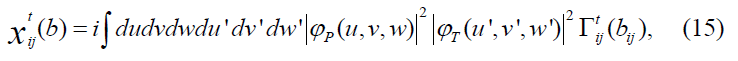
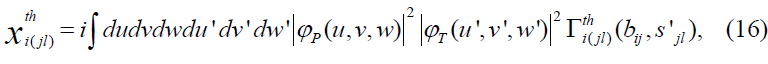
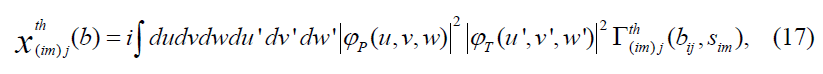
In these integrals

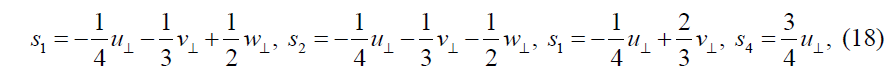
and similar relations for means the projection on the impact plane.

Using the equation (2) and expansion of 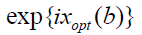as an infinite series, we get

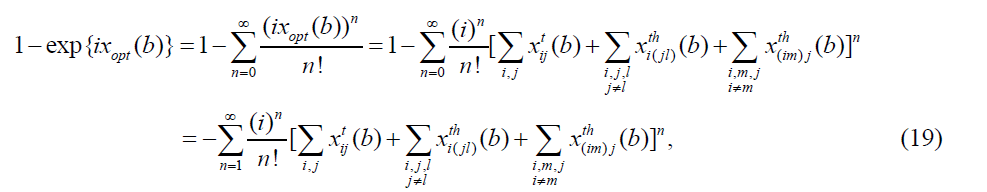
The first term in (19) where n=1, from equations (15), (16) and (17), is

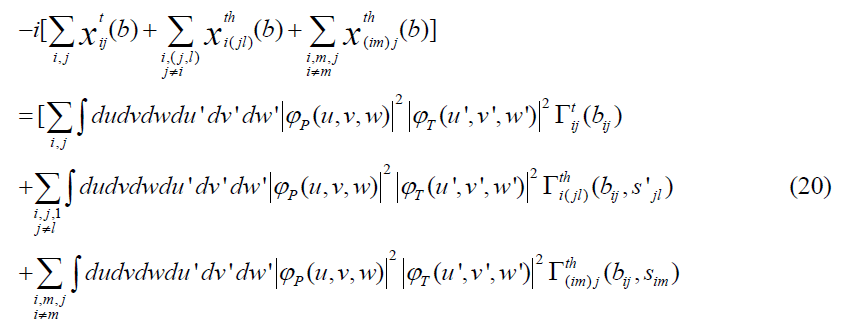
which represents the single scattering processes. It is clear that the first term in (20) represents the single scattering without the three-nucleon force correction. The second term represents the single scattering with the three-nucleon force correction which is coming from the target nucleons and the last term represents the single scattering with the three-nucleon force correction which is coming from the incident nucleons. At the same time, we can say that the first term in equation (16), i.e. equation (17), is the first order approximation inside the optical limit approximation. The other terms in the expansion (16) with higher orders do not represent multi-scattering terms. They are only corrections to the first approximation. These phase shifts are obtained analytically and the long formulas of phase shifts and elastic scattering amplitude F(q) cannot be presented here.

The α-⁴He elastic scattering differential cross section is calculated using the relation

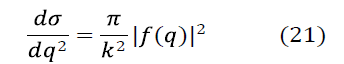
and the calculations performed up to the fifteenth order of expansion (19). The higher orders after tenth order do not have any effects, approximately.

Results and Discussion

The differential cross sections of α^-4He elastic scattering at 4.32 GeV/c, 5.07 GeV/c and 7 GeV/c are calculated including three-nucleon force in the optical limit phase shift function. For the three nucleon force parameters we will assume that A_(im)j=A_i(jl)=A and B_(im)j=B_i(jl)=B for all I, j, l, m [17,18]. The values of nucleon-nucleon parameters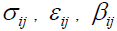 are taken from [10] where 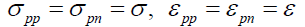and 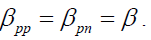β . These values and the three nucleon force parameters A and B are given in the Table 1.

Table 1: Nucleon-nucleon and three-nucleon force parameters. The values of nucleon-nucleon parameters at 4.32 GeV/c, 5.07 GeV/c and 7 GeV/c are taken from [10]. A and B are fitting parameters.

The results of the calculations with the parameter values in Table 1 are presented in Figure 1 for the momenta 4.32 GeV/c, 5.07 GeV/c and 7 GeV/c, respectively. The solid and the dashed curves represent the results of optical limit approximation with and without three-nucleon force. It is clear that, the dashed curve can describe the data in the forward direction where 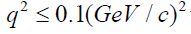for 4.32 GeV/c and 5.07 GeV/c and for 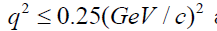at 7 GeV/c. In general, out of these ranges for q² the two-nucleon calculations are in disagreement with the experimental data and we need another effect to obtain an agreement with the data in these ranges. In fact, the low values of the differential cross section in the optical limit approximation, where the two-nucleon force is only considered, is due to the absence of multi-scattering terms. But this is not the only reason for the disagreement with the experimental data. For example, in the framework of Glauber multiple scattering theory with twonucleon force only, α^-4He elastic scattering calculations at the energy of order 1 GeV, are in disagreement with the data for 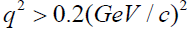[18]. The agreement was obtained by inclusion of the three-nucleon force.

To calculate the three-nucleon force contributions, the values of the parameters A and B in the Table 1 are used. These values give a better agreement with the differential cross section data. To calculate the three-nucleon force parameter γ, we consider the uncertainty relation of energy and time △ △ ≥ ℎ for 2π exchange three-nucleon force. In this case we take

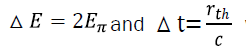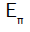where is the mass of π meson particle and r_th is the radius of three-nucleon force. Therefore, 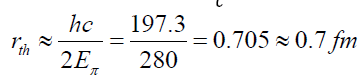At the same time, from the profile function of the three-nucleon force we can consider 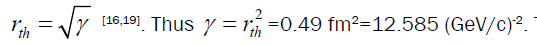This value of γ is independent of energy.

The results of calculations for (two-nucleon+three-nucleon forces) of α^-4He elastic scattering differential cross section are presented by solid curve in Figure 1 at 4.32 GeV/c, 5.07 GeV/c and 7 GeV/c, respectively. It is clear that, the three-nucleon force effect is clear and important to obtain an agreement with the experimental data, especially for 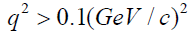at all momenta. In general, the obtained results prove the importance of three-nucleon force as well as the usefulness of the used approach.

Figure 1: α^-4He elastic scattering differential cross section at 4.32 GeV/c, 5.05 GeV/c and 7 GeV/c is presented. The solid and dashed curves represent the results with and without three-nucleon force, respectively. The data at 4.32 GeV/c and 5.05 GeV/c are taken from [11] and at 7 GeV/c are taken from [8].

Finally, we try to discuss the value of slope parameter of nucleon-nucleon scattering amplitude. We try to consider the determination method of slope based on the radius of nucleon-nucleon interaction. This radius rt is related to the mass of the field particle of strong interaction, π- meson, through the uncertainty relation of time and energy, where we can get 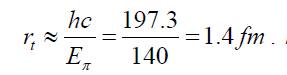At the same time, from the two-nucleon force profile function, equation (6), we can consider 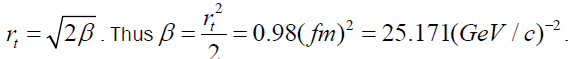This value of slope parameter is considered large with respect to the values which are used at the medium energies [6, 10]. However, with decreasing the slope parameter the radius of interaction decreases. For example, from the relation 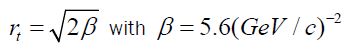[10], we get r_t =0.66 fm. Thus, the mass of field particle is 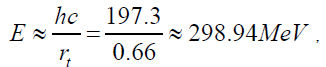which is not acceptable in the meson theory for strong force between nucleons.

It is intriguing yet the results of nucleus-nucleus (α^-4He) elastic scattering differential cross section at the considered medium energies with the large value of the slope parameter 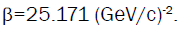The results of calculations with the same other nucleonnucleon parameters of Table 1 are given in Figure 2. The parameters A and B of Figure 2 are greater than this parameter of Figure 1. But, they are of the same order, approximately, See Table2.

Figure 2: Same as figure 1, except the value of the slope parameter, β _pp = β _pn = β = 25.171(GeV/c)^-2.

From Figure 2 and Table 2, where the values of x² for each case are given, we can see that the results with large value of slope parameter are slightly improved from the results of Figure 1, where the values of slope parameter are relatively small. In order to feel this improvement clearly, we can look at the Figure 3, where the results of (two-nucleon force + three nucleon force) are presented in the two cases.

Table 2. Values at different momenta for the two cases of slope parameter.

The difference between the results of Figure 1 and of Figure 2 is clear in the case of two nucleon force calculations, the dashed curves in both figures. The differential cross section with large value of slope parameter and two-nucleon force only is clearly lower than the corresponding results of Figure 1. This is because the large value of the slope parameter leads to a quick decrease of the two-nucleon force profile function. Therefore, we have lower values for the differential cross section. The increase of the three-nucleon force parameters (A, B) is to compensate the decrease in the two-nucleon force cross section. However, the shapes of the dashed curves in both figures are similar.

Now, we have a principal question: Which of the slope parameter values can be used? The value taken from the data of two free nucleons scattering, or that related to the general concept considering the meson theory. Especially, the differential cross section results of the second case are, in general, slightly improved from the results of the first case, see Figure 3.

Figure 3: T he solid curve represents the results with the slope parameter values of Table 1. The dot-dashed curve represents the results with the value β=25.171(GeV/c)^-2. In both cases the three-nucleon force is considered..

To ensure the accuracy of the results in both cases of slope parameter, the x² values at different momenta are calculated, see Table 2. The relatively small values of x² at the two momenta 4.32 GeV/c and 5.07 GeV/c for β = 25.171(GeV / c)⁻² are clear. At the same time, for this value of slope parameter, the x² value is relatively large at 7 GeV/c. This may be due to the wide range of q² ,0 < q² ≤ 4(GeV / c)² with large number of data points..

Summary

In the framework of optical limit approximation with inclusion of the three-nucleon force effect we obtained a reasonable agreement with the experimental data of α^-4He elastic scattering differential cross section at incident momenta 4.32 GeV/c, 5.07 GeV/c and 7 GeV/c. The three-nucleon force contributions are clear at all values of q². A relation between the radius of two-nucleon interaction and the slope parameter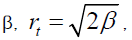 is used to calculate the value of β for any two nucleons and at any energy. With the value of β which is calculated by this way, we have for the differential cross section with three-nucleon force inclusion improved results from the case of different values of β at different energies. With the formula 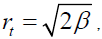we have an explicit physical basis to calculate unique value of the slope parameter at all energies, assuming that the radius of two-nucleon interaction does not change with energy.

References

1. Glauber RJ. Lectures on theoretical physics. Intersci. 1959;1:315.
2. Franco V. High energy nucleus-nucleus collisions: General theory and applications to deuteron-deuteron scattering. Phys Rev. 1968;175:1376.
3. Czyż W and Maximon LC. High energy, small angle elastic scattering of strongly interacting composite particles. Ann Phys. 1969;52:59-121.
4. Czyż W and Maximon LC. Coulomb effects in high energy He4α-He4 elastic scattering. Ann Phys. 1970;60:484.
5. Franco V and Varma GK. Collisions between composite particles at medium and high energies. Phys Rev. 1978;18:349.
6. Varma GK. Scattering of α-particles at medium energies. Nucl Phys. 1978;294:465.
7. Viollier RD and Turtschi E. Elastic scattering of heavy ions at high-energies. Ann Phys. 1980;124:290.
8. Satta L, et al. Elastic scattering of alpha particles on light nuclei at P(α)=7-GeV/C. Phys Lett B. 1984;139:263.
9. Franco V and Yin Y. Elastic scattering of α particles and the phase of the nucleon-nucleon scattering amplitude. Phys Rev Lett. 1985;55:1059.
10. Franco V and Yin Y. Elastic collisions between light nuclei and the phase variation of the nucleon-nucleon scattering amplitude. Phys Rev. 1986;34:608.
11. Berger J, et al.  αα elastic scattering at 4.32 GeV/c and 5.07 GeV/c. Nucl Phys. 1980;338: 421.
12. Usmani AA, et al. α4He elastic scattering at high energies. Phys Rev. 1989;39:1182.
13. Usmani AA, et al. 4He-4He elastic scattering and variational wave functions. Phys Rev. 1992;45:396.
14. Hassan MA, et al. Time-ordering effect in proton-nucleus elastic scattering. Ind J Phys. 2019;93:1069.
15. Hassan MA, et al. Approach for the three-body force effect in a high-energy approximation: Application to hadron-deuteron elastic scattering. Phys Rev. 2001;63:04606.
16. Hassan MA, et al. Approach for the three-body force effect in the optical limit approximation: Application to hadron-deuteron elastic scattering at high energies. J Phys G Nucl. 2013;40:065102.
17. Hassan MA and Salama TNE. p-3 He elastic scattering at 0.6 GeV-1 GeV: some short-range effects. Ind J Phys. 2015;89:829-834.
18. Hassan MA, et al. Proton-4He elastic scattering at 350-1728 MeV energies: Three-body force effect. Int J Mod Phys. 2018;27:1850020.
19. Hassan MA, et al. Three-quark force in p-p elastic scattering. Eur Phys J. 2018;78:1029.
20. Hassan MA, et al. Three-quark force effect in proton-proton scattering at 7 TeV, 8 TeV and 13 TeV. Eur Phys J. 2019;79:599.
21. Caurier E and Navrátil P. Proton radii of 4,6,8He isotopes from high-precision nucleon-nucleon interactions. Phys Rev. 2006;73:021302.
22. Alhagaish I, et al. Ground state properties of 4He and 12C nuclei at equilibrium and at large static compression at zero temperature using Nijmegen and Reid soft core nucleon-nucleon interactions. arXiv:1803.04650v1. 2018.