Variation of Phase Shift and Energy Gap in Nuclear Matter

Abstract

Using a nucleon-nucleon exponential interaction potential V (r ) = -V0 exp (-2r / β) an expression for phase shift, δl (kf) , has been obtained omitting iso-spin effects. For Fermi momentum 0fm −1 , 0.1 fm −1 , 0.2 fm −1 … the values of phase shift, δl (kf) , have been calculated. The values of the phase shift, δl (kf), increase linearly with the increase in Fermi momentum, kf .The expression for the energy gap, Δ (kf) , and its variation with Fermi momentum f k , is also calculated. The results obtained are found to be in agreement with Gezerlis.

Keywords

Phase Shift, Nuclear Matter, Energy gap, Fermi momentum.

Introduction

Most of what we know about nuclear pairing comes from nuclei with a sizable neutron excess where the isospin T = 1. Neutron-neutron (nn) and proton-proton (pp) pairing dominate [3]. The nuclear force has been at the heart of nuclear physics ever since the field was born in 1932 with the discovery of the neutron by Chadwick [1]. In fact, during the first few decades of nuclear physics, the term nuclear force was often used as synonymous for nuclear physics as a whole. The interaction between two nucleons is basic for all of nuclear physics. The traditional goal of nuclear physics is to understand the properties of atomic nuclei in terms of the bare interaction between pairs of nucleons.

The oldest theory of nuclear forces was presented by Yukawa based on the model in which the mesons mediate the NN (pp, pn, nn) interactions. The interaction between nucleons is characterized by the existence of a strongly repulsive core at short distance with a characteristic radius ≈ 0.5 −1fm . The interaction obeys several fundamental symmetries such as translational, rotational, spatial-reflection, time-reversal invariance and exchange symmetry. General quantum numbers of a two-nucleon system is a natural starting point for a discussion of pairing found in nuclei [3].

It is not easy to precisely construct a nucleon-nucleon interaction. However, a description of the interaction in terms of various meson exchanges is at present the most quantitative representation in the energy regime of nuclear physics.

It can be assumed that the meson exchange is an appropriate picture at low and intermediate energies and that at present it is sufficient to limit attention to the time-honoured configuration space version of the nucleon-nucleon interaction [4], including only central, 1, spin-spin, ó . ó , tensor, 12 S r,and spin-orbit, L.S, terms . When two nuclear particles or two nucleons collide with each other or scatter, there is what is called a scattering length, , the distance of the nearest approach. Once the particles are in the field of force of each other, they interact and scatter in any direction resulting in a phase shift or phase difference,δ_l (k_f) .Thus phase shift, δ_l (k_f) ,depends upon the interaction potential. We consider 1SO pairing in infinite neutron matter and nuclear matter and show that in the lowest order approximation, where the pairing interaction is taken to be the bare nucleon-nucleon interaction in the 1S0 channel, the pairing interaction can be determined directly from the 1S0 phase shifts.

Many attempts have been made to derive an effective formula for calculating the phase shift in large nuclear systems using a nucleon-nucleon interaction in a given shell-model space and bare nucleon-nucleon interaction using many-body perturbation theory [3]. While some theories appeared to work well for some nuclei, there are several indications that these formulae fail to produce results that can be compared with experimental values [5,6]. A formula is derived that is used to find the values of the energy gap, Δ (k_f) , and phase shift, δ_l (k_f) ,also a formula has been derived which correlates phase shift, δ_l (k_f) , and energy gap using some known nucleon-nucleon interactions.

Pairing In Nuclear Matter

There has been renewed interest in the pairing problem in neutron matter and neutron-rich nuclei. The pairing gap is determined by the attractive part of the NN interaction. For the 1S0 channel in nuclear physics, depending upon the number of neutrons, when there is a nucleon-nucleon interaction such that their spins are aligned opposite, the angular momentum is zero. The channel for such neutron excess will be 1S0. There are two weak coupling limits. One is when the potential is weak and attractive for large inter-particle spacing and second when the potential becomes repulsive at the inter-particle distance, r, 0.6 fm. The potential has a value of some fewMeV . In the strong coupling limit, the nucleon-nucleon potential is large and attractive; its value reaches a maximum of around 100 MeV at r ≈1 fm.

In the 1S0 channel the potential is attractive for momenta k ≤ 1.74 fm⁻¹ (or for interparticle distances r ≥ 0.6 fm). In the weak coupling regime, where the interaction is weak, attractive and the coherence length is larger than the interparticle spacing, a gas of fermions may undergo a superconducting (or superfluid) instability at low temperatures, and a gas of Cooper pairs is formed. This gas of Cooper pairs will be surrounded by unpaired fermions and the typical coherence length is large compared with the interparticle spacing, and the bound pairs overlap.

In the strong-coupling limit, the formed bound pairs have only a small overlap, the coherence length is small, and the bound pairs can be treated as a gas of point bosons. One expects then the system to undergo Bose-Einstein condensation into a single quantum state with total momentum k = 0 , called the zero-momentum state [7]. For the1S0 channel in nuclear physics, we may actually expect to have two weak-coupling limits, namely when the potential is weak and attractive for large interparticle spacing and when the potential becomes repulsive at r ≈ 0.6 fm . In these regimes, the potential has values of the order of some fewMeV .

One may also consider a strong-coupling limit where the N potential is large and attractive. This takes place where the N potential reaches its maximum, with an absolute value of typically ∼ 100MeV , at roughly ∼1fm . We note that fermion pairs in the1S0 wave in neutron and nuclear matter will not undergo the above-mentioned Bose-Einstein condensation, since, even though N the potential is large and attractive for certain Fermi momenta, the coherence length will always be larger than the interparticle spacing, as demonstrated by De Balsio [8].

The inclusion of in-medium effects, such as screening terms, are expected to further reduce the pairing gap and thereby enhance further the coherence length. This does not imply that such a transition is not possible in nuclear matter. A recent analysis [9] of triplet 3S1 pairing in low-density symmetric and asymmetric nuclear matter indicates that such a transition is indeed possible.

It is found that the neutron pairing gap 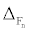is strongly dependent on the Fermi momentum, or equivalently, the nuclear matter density. Energy gap Δ (k_f) , increases as the Fermi momentum (or density) goes down, reaches a maximum at 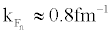in symmetric nuclear matter or 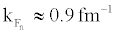in pure neutron matter, and then rapidly drops to zero. A systematical enhancement of about 0.3MeV for Δ (k_f) around 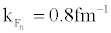is revealed in pure neutron matter compared with those in symmetric nuclear matter for all of the adopted pairing interactions [10].

The energy gap is to a remarkable extent determined by the available 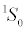phase shifts. Thus, the quantitative features of 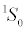pairing in neutron matter can be obtained directly from the 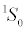phase shifts. This happens because the N interaction is very nearly separable in this channel due to the presence of a bound state at zero energy, even for densities as high as, 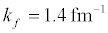This explains why all bare N interactions give nearly identical results for the 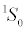energy gap in lowest-order BCS calculations.

The results of different groups are in close agreement on the 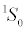energy gap values and on its density dependence, which shows a peak value of about 3MeV at a Fermi momentum close to 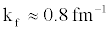[4]. All these calculations adopt the bare N interaction as the pairing force, and it has been pointed out that the screening by the medium of the interaction could strongly reduce the pairing strength in this channel [11]. The issue of the many-body calculation of the pairing effective interaction is a complex one and still far from a satisfactory solution.

The calculation of the 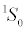gap in symmetric nuclear matter is closely related to the one for neutron matter. Even with modern charge-dependent interactions, the resulting pairing gaps for this partial wave are fairly similar [4].

The size of the neutron-proton (np)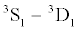 energy gap in symmetric or asymmetric nuclear matter has, however, been a much debated issue since the first calculations of this quantity appeared. While solutions of the BCSequations with bare nucleonnucleon N forces give a large energy gap of several MeVs at the saturation density 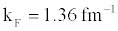[12-14], there is little empirical evidence from finite nuclei for such strong np pairing correlations, except possibly for isospin T=0 and N=Z.

Since the pairing correlations are largest for small densities, i.e., at the surface of the nucleus, this result agrees with the usual observation that pairing in nuclei is a surface phenomenon. Moreover, the agreement between the results obtained with bare relativistic forces and those obtained with the force for the pairing properties of the symmetric nuclear matter is a particularly interesting outcome as in that using this density dependence of the gap parameter in semi classical calculations the average pairing properties of finite nuclei can be reproduced rather well [15].

Following the discovery of neutron stars, calculated gaps for neutron matter within the BCS theory using a separable nucleonnucleon interaction that had been fitted to two-nucleon scattering data. Their calculations predicted a pairing gap for neutrons in the 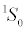state that first rose with increasing density, reached a maximum of roughly 3MeV at a density of about 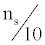, where 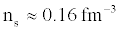is the saturation density of nuclear matter with equal numbers of neutrons and protons, a density typical of the interiors of heavy nuclei. With further increase in density, the gap dropped and vanished at a density somewhat below n_s .

The qualitative behavior of the gaps may be understood in terms of the measured phase shifts for nucleon-nucleon interactions. A positive phase shift corresponds to an attractive interaction between neutrons, and therefore at low k, which corresponds to low Fermi momentum and low density, the most attractive channel is 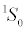, [3,4]

The main objective of this paper is to establish the correlation between the Phase Shift, δ_l (k_f) , against Fermi momentum, , k_f , and Energy Gap, Δ(k_f) , against Fermi momentum, k_f ,using the exponential potential in Nuclear Systems.

Theoretical Formulations

At a low density limit a general two-body Hamiltonian for an assembly in the ground state can be written as [3]

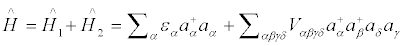
where 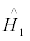represents the kinetic energy of the system, 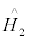represents the potential energy of the system, a + is the fermion creation operator, a is the fermion annihilation operator, V_αβγδ represents the coupled matrix elements of the two-body interaction V(r). The sums run over all possible single-particle quantum numbers.

With in the meson-exchange models, we may have exchange of π, ρ, ω, σ, η and δ mesons. As an example, for a potential due to the exchange of a π -meson, the co-efficient C_σ = C_T =(g2NN π/4π ) (m3π/12M2); and 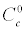= = 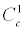= 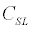0 with experimental value for g2NN π ≈13.5, mπ is the mass of the π-meson, M is the mass of the nucleon [16,17]

The complete interaction is written as [3]

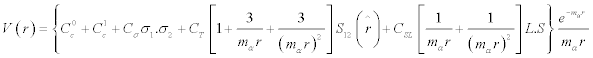(2)

where m_σ is the mass of the relevant meson and S₁₂ is due to the tensor force term; such that

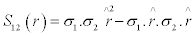
Where σ is the standard operator notation for spin -1/2 particles.

From discussion of the potential due to the exchange of a π –meson, the co-efficient Cσ = CSL =(g2NN π/4π) (m3π/12M2); 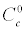= = 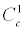= 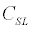0 with experimental value for g2NN π≈ 13.5, the interaction potential, V(r) therefore, reduces to 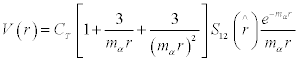[3]

(3)

Other potentials that may be used [1] are,

Square well potential,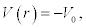

Gaussian well potential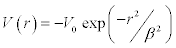

Yukawa well potential,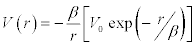

Exponential well potential,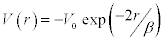

where V(r) is the interaction potential, r is the inter-particle distance, β is the range of nucleon-nucleon force and 0 V is the potential well depth.

Calculations are done to correlate the interaction potential v(r), to the phase shift, δ_l (k) and energy gap, Δ (k_f)

The exponential potential 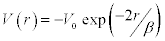is used in our derivation of phase shift and energy gap equations, since it has not been much explored by other researchers like the Gaussian well potential and Yukawa well potential [1].

The Born-approximation expression for phase shifts, δ_l (k_f) , for scattering from a spherical potential,V(r), in 3-D is given by, [2]

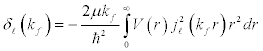(4)

Equation [4] is used in calculating the phase shift, δ_l (k_f), by using the exponential potential given as 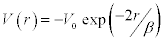and using Bessel Function in the form 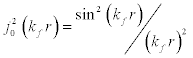for ℓ=0, ground state, where 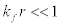. (5)

Using derived equations and the values of the constants available, data was then generated and tabulated. Graphs have been drawn to show how the phase shift δ_l (k_f) varies with the Fermi momentum, k_f .This potential is substituted in the Bornapproximation phase shifts, δ_l (k_f) , for scattering from a spherical potential, V(r), in 3-D, and to find the values of phase shifts.

The pairing gap for small values of 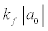is (Dean and Hjorth-Jensen, 2003; Gorkov and Melik-Barkhudarov, 1961),

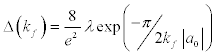(6)

where a₀ is the scattering length in the 1S0 channel ( a₀ = -23.7 fm), λ is a constant ≈1, e = 2.718 . Here a₀ is related to the interaction potential between a pair of nucleons. However, at saturation density ρ₀ = 0.17 fm-3, f k =1.36 fm-1.

For low energy scattering, especially in nuclear physics, the phase shift, δ_l (k_f), due to scattering is given by the relation [2,4].

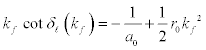(7)

here 0 r is the effective range of the nuclear force which roughly corresponds to the size of the potential and δ_l (k_f) is the S-wave scattering phase-shift

At ground state 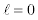therefore Eq. [4] becomes,

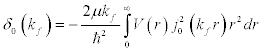(8)

here 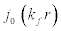is the spherical Bessel function of zeroth order i.e. ℓ= 0 such that,

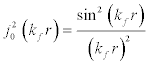(9)

It is valid to represent the interaction energy of a particle with momentum i f 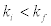, with all the particles within the Fermi surface. The values for i k could be 0.1fm-1, 0.2fm-1, 0.3fm-1… (Khanna & Barhai, 1975) and therefore for 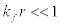, hence 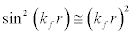therefore Eq. [9] reduces to,

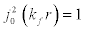(10)

Substituting the value of the exponential potential, 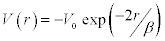, and that of 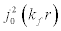from Eq.[10] in Eq. [4], we get,

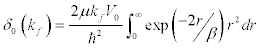(11)

Integrating Eq. [11] by parts we get,

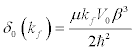(12)

Now for exponential potential, the value of the well-depth parameter, s ,is [1]

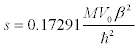(13)

where M is the average mass of the two interacting nucleons, 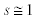for the bound state of the nuclear matter; and hence V0 is given by,

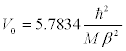(14)

Substituting Eq. [14] in Eq. [12] we have,

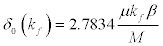(15)

Now in the exponential potential, the range of the potential well, V0 , is, b , and, β, are related by the relation,

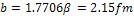(16)

Therefore β = 1.2143 fm , for 1S0 scattering, and the reduced mass,μ , of the two interacting nucleons is given by

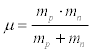(17)

where m_p the proton is mass equal to 938.27Mev , and m_n is the neutron mass equal to 939.57Mev . Substituting the values of the masses in Eq. [17] we have the reduced mass μ = 469.46Mev . The average mass M of the proton and neutron is given by the equation,

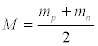(18)

Substituting for the value of the masses M = 938.92Mev , then Eq.[15] becomes

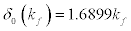(19)

We will calculate the values of phase shift, 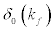, for different values of f k ranging from 0.1 fm⁻¹ , 0.2 fm⁻¹ ,0.3 fm⁻¹ ,…1.6 fm⁻¹ , and plot a graph of phase shift, 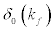, against Fermi momentum, k_f ,.

For scattering length in the 1S0 channel, a₀ = −23.7fm , e = 2.718 and λ ≈ 1 Eq.[6] for energy gap, Δ (k_f) , becomes,

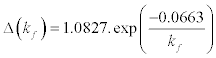(20)

Eq. [20] will give the values of energy gap, Δ (k_f) , for different values of the Fermi momentum, k_f.

Results and Discussion

Equation [19] is used to compute the values of phase shift, δ₀ (k_f) , against changes in the Fermi momentum, k_f , and this variation, is studied using MathCAD 2000 Professional software and data tabulated as shown in Table 1.

Table 1. Values of Phase Shift against the values of Fermi Momentum.

The following graph is obtained from Table 1.

When the Fermi momentum, k_f , of the interacting nucleons is zero the value of phase shift, 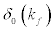, is equal to zero in the ground state as seen from Figure 1. This shows that an increase in Fermi momentum, k_f , leads to an increase in phase shift, .

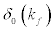Equation [19] is used to compute the values of energy gap, Δ(k_f ) , against changes in the Fermi momentum, k_f , and this variation is studied using MathCAD 2000 Professional software and the data tabulated as shown in Table 2.

Table 2. Values of energy gap against the values of Fermi momentum.

The following graph is obtained from Table 2 (Figure 2).

The energy gap, Δ(k_f ), increases steadily and faster for low Fermi momentum, k_f , upto around 0.4 fm⁻¹ and it is roughly constant with a value ≅ 1.0MeV for 0.4 fm 1 k_f > − .In literature the values of the energy gap, Δ(k_f ) , are 0.2 MeV, 0.4 MeV, 0.6 MeV... for 0.2 fm⁻¹ , 0.3 fm⁻¹ , 0.4 fm⁻¹ … respectively [18] which are in agreement with the values known so far in the trend see Table 2.The reason for the good agreement is that, for calculating energy gaps, the quantity that matters is the scattering length at energies of order of the Fermi momentum, and this is strongly constrained by nucleon-nucleon scattering data for nucleon momenta in the center-of-mass. For higher Fermi momenta the energy gap tend to reach saturation since, there is considerable model dependence, also because inelastic channels start to open up in nucleon-nucleon scattering. When two nuclear particles or two nucleons collide with each other or scatter, there is what is called a scattering length, a₀, the distance of the nearest approach. Once the particles are in the field of force of each other, they interact and scatter in any direction resulting in a phase shift or phase difference, δ_l (k_f) , thus phase shift, Δ(k_f ) δ , depends upon the interaction potential, V(r). Considering 1S0 pairing in infinite neutron matter and nuclear matter and the bare nucleon-nucleon exponential interaction in the 1S0 channel, our calculations shows that the phase shift, δ_l (k_f) , increases linearly with Fermi momentum, k_f .The energy gap, Δ(k_f ) , increases steadily and faster for low values of Fermi momentum, k_f ,and become roughly constant for values of 0.4 fm 1 f k > − . It will be interesting to see that if other potentials are used, for instance, the potential used Hassan and Ramadan study [19], how phase shift, δ_l (k_f), and energy gap, Δ(k_f ) , vary with Fermi momentum,k_f .

Acknowledgments

We appreciate the discussions with colleagues at the department of physics during the preparation of this manuscript. A lot of gratitude also goes to the International Centre for Theoretical Physics for availing to us some articles through their eJDS platform.

References

1. Blatt JM and Weisskoff VK. Theoretical Nuclear Physics1952Newyork, John willeysons.
2. GezerlisA et al. Pairing and super fluidity of nucleons in neutron stars.2014; 2: 1-48.
3. Dean DJ andHjorth-Jensen M. Pairing in Nuclear systems: From neutron stars to finite nuclei. Rev. Mod. Phys. 2003; 75: 607.
4. Elgarøy Q andHjorth-Jensen M. Nucleon-nucleon phase Shifts and Pairing in Neutron matter and Nuclear Matter.Phys. Rev. C,1997; 57: 1174.
5. Pudliner BS et al. Quantum Monte Carlo calculations of nuclei with A<~ 7. Phys. Rev. C. 1997; 56.
6. Gregory P et al. Pairing Interaction and Two-Nucleon Transfer Reactions.Nuclear Physics New. 2014; 24: 19-25.
7. Nozieres P and Schmitt-Rink S. Bose Condensation in attractive fermion: from weak to strong coupling superconductivity. Low Temperature Physics.1985; 59:195-211.
8. De Blasio FV et al.Nonperturbative study of the damping of giant resonances in hot nuclei. Phys. Rev. Lett. 1992; 68: 1663.
9. Lombardo U et al. Transition from BCS pairing to Bose-Eistein Condensation in-low-density asymmetric Nuclear matter. Phys. Rev. C: Nuclear physics. 2001; 64.
10. Bao YS and Wei P.Dineutron correlations and BCS-BEC crossover in nuclear matter with the Gogny pairing force. Nuclear Physics A. 2013; 909: 8–19.
11. Chen M. Review of particle physics. Phys. Rev. lett. B. 2008; 667: 1–6.
12. Akmal A et al. Equation of State of Nucleon Matter and Neutron Star Structure. Phys.Rev. C. 1998; 58: 1804.
13. Takatsuka T and Tamagaki R. Nucleon superconductivity in neutron star core progress direct URCA cooling.Prog. oftheor. phys. 1997;97: 345-350.
14. Vonderfechta BE et al. Influence of Tensor and Short-range Correlations on Nucleon Properties in Nuclear Medium. Nucl. Phys. A. 1993; 555: 1-32.
15. Serra M et al. Relativistic theory of pairing in infinite nuclear matter. Phys. Rev. C. 2001; 65: 014304, 3.
16. Machleidt R et al. Nonlocal Nature of the Nuclear Force and its Impact on Nuclear Structure. Phys. Rev. C; Nuclear Physics. 1996; 53.
17. Stoks VGJ et al. Accurate Nucleon-Nucleon Potential Charge-independence Breaking. Phys. Rev. C. 1995; 51: 38.
18. Khanna KM and Barhai PK. Single-particle potential, rearrangement energy and effective mass of nuclear matter, 208Pb and 16O. Nuclear Physics A. 1975; 243: 298-308.
19. Hassan MYM and Ramadan S. On the properties of nuclear matter with an excess of neutrons, spin-up neutrons and spin-up protons using effective nucleon-nucleon potential, ActaPhysicaPolonica. 1978; B9: 989.