Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
1College of Electronic Science and Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, China.
2School of Computer Science, Nanjing University of Science and Technology, Nanjing 210094, China.
3Jiangsu Province Engineering Lab of RF Integration and Micropackage, Nanjing 210003, China.
Received: 08/28/2015 Accepted: 10/28/2015 Published: 10/30/2015
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Heart sound is an important physiological signal, and it contains a large number of physiological and pathological information. According to the characteristics of heart sound, the symbol entropy based on probability distribution is proposed. The algorithm makes a breakthrough at linear constraints. On the one hand, it distributes more symbols for the region where the amplitude distribution of the first heart is dense and distributes relatively less symbols for the sparse region, so as to achieve the reduction of redundancy of data; On the other hand, it use an self-adaptive method to determine the size of the symbol set. Then the symbol entropy becomes more sensitive to the changes of the heart sound signal and could capture rapidly the nonlinear abnormal state of heart signal. Thus the algorithm can make little or no impact of the non-stationary mutation interference and the sequence probability distribution on the entropy. Simulation results show that the algorithm not only has significant feasibility and effectiveness but also provides a new way for the rapid diagnosis of heart failure.
Biophysics, Heart sound, Symbol entropy, Probability distribution.
It is a kind of important means to do research on various physiological signals for the disease diagnosis and treatment. Heart sound signal is one kind of internal signal, one of the most important physiological signals. There is a very long history for its application in auscultation and adjuvant therapy [1]. Heart sound is compound sound of mechanical vibration, and it contains different parts of the heart (such as the atrium and ventricle, blood vessels and heart valve) functional status of a large number of physiological and pathological information, which directly reflects the mechanical movement status of large blood vessels and heart system and closely related to human pathology. Testing and analysis of heart sound signals in the clinical medicine practice has important application value.
The time series of biological signal contains complex fluctuations, which is a kind of external manifestation of the body's physiological system activity state. Disease and aging process reduce the ability of the human physiological system to adapt to the external environment, so that the amount of information contained in the time sequence changes [2]. But the understanding of physical activity is not fully clear. In order to get more detailed understanding of the body's physiological activity, we needs a variety of experiments and the deep study on the time series analysis method.
The relationship between heart sound and cardiac muscle contraction ability both at home and abroad have been studied. Rice and Doyle after lots of experiments demonstrates the size of the first heart sound amplitude has close relationship with myocardial contraction ability, and monitor effect of anesthetic on myocardial contraction force of patients in the operating room with a heart sound detection instrument[3]. Sun proposes an effective method to evaluate cardiac function by discussing the relationship between the first heart sound amplitude and the myocardial systolic function [4]. Bu’s studies shows that myocardial contra ction force variation can be described by the first heart sound amplitude fluctuation signal [5]. This fluctuation signal contains a lot of heart physiological and pathological information, and the research of the fluctuation trend to assess the ability of myocardial contraction of the heart, to deepen the understanding of the mechanisms of cardiac autonomic nerve.
In recent years, through continuous exploration, a variety of methods to measure the complexity of the nonlinear time series have been proposed, such as correlation dimension, Lyapunov index, sample entropy and nonlinear prediction, etc. [6]. However, these methods have restrictive condition in using. Such as, correlation dimension and Lyapunov index, must request the length of time series is long enough. Time series of local trends will affect the sample entropy, the possibility of the original data.
Traditional sample entropy is affected by threshold value and probability distribution, in order to reduce the non-stationary mutation interference and the influence of the probability distribution of sample entropy, literature [7] combine symbolic dynamics and sample entropy, symbolic samples such as probability entropy is proposed. Symbolic time series analysis, a kind of nonlinear analysis method, is based on the theory of symbolic dynamics and the chaotic sequence analysis. Its essence is to coarse graining on the time series in the amplitude domain, i.e., map analog quantity of the amplitude domain to symbol set which consists of a finite number of symbols, and then do dynamics analysis on the converted symbol sequence. Although in the process of symbolization it will lose some details, this kind of treatment can significantly improve the operation speed. At the same time, if the symbolic methods selection is appropriate, it not only can reflect the dynamic characteristics of the original time series, but also can greatly reduce the effects of noise. So in symbolic dynamics analysis, the most critical step is how to use the original time series to determine the appropriate symbol zoning, and make sure the guarantee of dynamic characteristics of a signal without loss of the original sequence.
According to the characteristics of heart sound time sequence and related theory of nonlinear analysis, this paper puts forward a kind of Symbol Entropy Based on Probability Distribution (PDSE) algorithm. The algorithm aims to achieve: 1, The heart sound symbol sequence can completely reflect the timing sequence relations of heart sounds original sequence, and eliminate effect of heart sound original sequence probability distribution to symbolic process; 2, Use self-adaption means to decide the size of the symbol set in the process of symbolization, and the purpose of the self-adaption is to distribute more symbols in the first heart sound amplitude comparatively dense distribution region, fewer symbols in a relatively sparse area, which can break through the traditional uniform symbolic linear constraints, and reduce the data redundancy and improve the utilization rate of symbols. Obviously, this kind of targeted algorithm makes the symbol entropy more sensitive to the change of heart sounds data and can capture nonlinear abnormal state of heart sound signals quickly. The simulation results show that the proposed algorithm has significant feasibility and effectiveness, and provides non-destructive diagnosis of heart failure with a new idea.
The adaptive symbolic methods for heart sound
A cycle of heart sound signals can be described as Equation 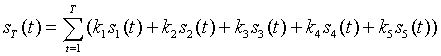(1):
(1)
Among, s1 , s2 is the first and second heart sound signals respectively;, s3 , s4 is the third and fourth heart sound signals respectively, while the study about them is relatively less; s5 is on behalf of the heart noise; k denote composite coefficient[8].
Heart sounds presents approximate cycle characteristics. Assuming that the first heart sound amplitude in cycle j is s1(j) , so first heart sound signal amplitude sequence x(i) within the scope of N cycle can be expressed as Equation 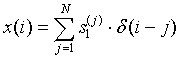(2):
(2)
Among it, δ(i) is unit sampling sequence. The gain of x(i) is on display in Figure 1. To mark the maximum value of first heart sound signal amplitude sequence in the normalization of heart sound signals, as shown in Figure 1a; To find the max value in the positive axis, as shown in Figure 1b.
Figure 1: The gain of the first heart sound amplitude for (a) S1 region, (b) the maximum value of S1.
The main problem of most heart failure patients has a connection with the declining ability of the myocardial contraction. Myocardial under the regulation of vagus nerve and sympathetic nerve will show the inotropic and chronotropic and conductivity characteristics in many aspects. Because any heart disease maybe develop to heart failure, so in the treatment of cardiovascular diseases during the early diagnosis of heart failure, the process of assessment of myocardial systolic function changes has important significance.
The first heart sound amplitude sequence within 1000 cardiac cycles is shown in Figure 2.
Figure 2: The wave pattern of the first heart sound amplitude sequence.
First of all, symbolize signals of little changes in amplitude, and then analyzes the symbol sequence by statistics processing. The basic idea of Symbol is depend on the given time data sequence, and marks each data point of time sequence with a symbol of symbol set.
A variety of symbolic algorithm is proposed in the literature at home and abroad, e.g., algorithm based on the maximum change cluster, the algorithm based on entropy, symbolic algorithm based on the symbol pseudo adjacent nodes, and the symbolic algorithm based on wavelet decomposition [9]. If the signal is evenly distributed, use the above methods to symbolization to get ideal result. From Figure 2, s1 amplitude sequence has non-uniform distribution characteristics. Most of the data values are in the range of 0.65 ~ 0.75, using the above method is not proper to the first heart sound amplitude sequence. Therefore this paper proposes an self-adaptive symbolic methods to improve the insufficient.
Assuming that amplitude sequence is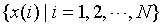 
, the corresponding symbol sequence is 
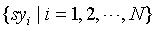, and size of the symbol set is n (the initial value is 1). The heart sound self-adaption symbolic steps are as follows:
Step 1: Array the size of amplitude of first heart sound amplitude sequence x(i) from small to large, sorting for interval Sec11 , do mathematical statistics, and probability density function f(x) can be got;
Step 2: Use the average of two endpoints of Sec11 to divide itself into two parts, execute n = n +1, get the new interval, in turn to each interval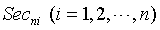
, two endpoint value of the interval i denoted as secni,l , secni,r
Step 3: According to the mapping relationship of n-number symbols, such as Equation (3) to symbolize sequence:
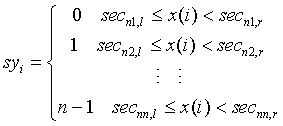(3)
Step 4: Generate sequence of symbols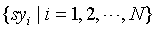 
and the length P of sequence set, a substring combinations, is expressed as 
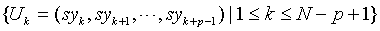. The number of substring combination is npwhich contains symbols 0, 1,..., n – 1. The number of occurrences of each substring is NT, and its probability is Equation 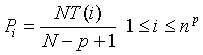(4):
(4)
Symbolic dynamics information entropy Sh decides whether to continue to divide, Sh can be obtained from the Equation (5) [10]
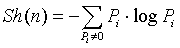(5)
Step 5: Make Equation (6)
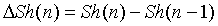
n ≥ 2 .. (6)
Select a threshold ε and ε > 0 If ΔSh ≤ ε , stop symbolic. Else, find i, which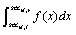 
can be max. Interval Secnican be divided into two parts by the average again, make n=n+1. Cancel the original classification and redistribution new symbols, repeat steps 3, 4, 5.
Symbolization is the main task of the set as much as possible with minimal symbol reserves the effective information system. Self-adaptive classification symbol, is the purpose of the distribution of more symbols to intensive interval amplitude distribution, distribution of fewer symbols to sparse data range, so as to make the information rich data intensive interval is more sensitive to changes in data, more conducive to capture nonlinear abnormal state of heart sound signals.
The parameter settings for heart sound signal
The self-adaption symbolic process is decided by N and ε . Sh can reflect the abundance and distribution characteristics of the substring after symbolization. With the increase of symbol set, the substring model will increase, and the distribution will be more dispersed, Sh will increase. Comprehensive consideration, choose a suitable threshold (when Sh increase amplitude is less than the given threshold, symbolic end) is necessary. The increase of Length of Substring p will lead to the increase of computation and data length, and it has no effect to the results. So, generally p is no less than 3, and p=3 in this paper. For length of the original sequence N, general requirements N = np .
Heart sound signals are approximate periodic weak physiological signal, and numerical distribution of first heart sound signal amplitude sequence is relatively concentrated. If properly selected, the threshold is going to get a good balance between algorithm performance and time complexity. Take a time for 1 hour heart sound signals, extract s1 amplitude sequence. Make ε =2, for the step length decreases down at 0.05 and get the scatterplot amplitude sequence, as is shown in Figure 3. From it, we can know when ε ≤ 0.45, n is stable. So, in self-adaptive symbolic process, ε =0.45.
Figure 3: The scatterplot of s1 amplitude sequence.
The self-adaptive symbolic algorithm applies not only to the heart sound signal, but also for no related completely random time sequence. Length of Gaussian white noise sequence is N, and size of symbolic set is N, make p = 3, and then we can get Equation (7) and Equation (8):
(7)
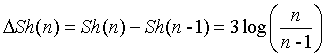(8)
n ≥ 2
In theory, for the Gaussian white noise sequence, the value of ΔSh can be described in Table 1, and theoretical curve is in Figure 4.
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ΔSh | 2.0794 | 1.2164 | 0.8630 | 0.6694 | 0.5470 | 0.4625 | 0.4006 | 0.3533 | 0.3161 |
Table 1: The value of ΔSh
Figure 4: The theoretical curve of ΔSh
Make the length of Gaussian white noise sequence is 3000, and the theoretical curve of ε − n is shown in Figure 5. Make ε separately is 0.33, 0.38, 0.43, 0.50, 0.60, 0.70, 1.0, 1.70 and we can get 8 red splashes, which illustrate the validity of the above theory. It is observed that the symbolization of the proposed method of symbolization has better statistical properties.
Figure 5: The theoretical curve of ε − n
Entropy algorithm based on the probability distribution
Symbol sequence analysis focuses on the analysis of each symbol, and extracts the implicit characteristics of cardiac kinetics system. Samples entropy use information increasing rate to depict the complexity of time series, and this paper combines self-adaptive symbolization and sample entropy to propose Symbol Entropy Based on Probability Distribution of symbols (PDSE).
Symbol entropy calculation method of symbol sequence is similar to the calculation of sample entropy method of the time series.
For the symbol sequence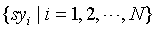 
, the algorithm of PDSE is as followed:
Step 1: Embed syi in m dimensional phase space, and we can obtain symbol vectors:
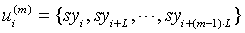
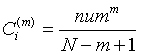
Among it [11] , L=1, m=3.
Step 2: For 1 ≤ i ≤ N − m
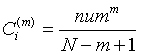(10)
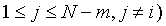
Among it, numm denotes the number of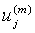 
which is equal to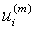
Step 3: Calculating the average of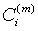 
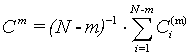
Step 4: Embedding dimension added to m+1, repeat steps 1, 2, 3,we can have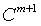 
, so:
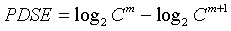
Multi-scale analysis
In order to break through the limitations of single scale symbol entropy, according to the characteristics of heart sound signal, first heart sound signal amplitude sequence can also be multi-scale analysis. Given the scale factor γ , we have [12]:
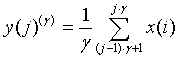
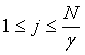
For the different γ , calculate the PDSE entropy of the new sequence y( j)(γ) .
The acquisition of experimental data
From our mind database select 40 cases of healthy heart sounds as health group (age:20~56), and from a hospital in Nanjing collect 36 patients with heart failure heart sounds as heart failure group (age:50~71). Collect heart sound by using physical invented the shoulder belt type of heart sounds collector (Figure 6) in the apex beat acquisition, and the core technology of the product has applied for the Chinese invention patent (patent number: public CN2013093000306700). Sampling frequency is 11025 hz, and sampling number is 16, and acquisition time is 45 minutes, the results are saved as wav format. The db6 wavelet is used to de-noise heart sound signal, and then each long heart sound signals are shortened to three 15 minutes, so there is a total of 228 cases of the experimental data.
Figure 6: Shoulder belt type heart sounds collector.
Extracting each first heart sounds signal amplitude sequence, by using the algorithm of PDSE we are able to evaluate each amplitude sequence complexity of heart sound level. As shown in Figure 7, the two sets of heart sound samples in different time scales on the complexity of the error bar graph.
From Figure 7, you can see that in the original scale, heart failure PDSE were significantly lower than healthy group, p < 0.01. Due to the low scale mainly represent signal of high frequency components and the high frequency components is mainly associated with the regulation of the vagus nerve of human body. It explains that the occurrence of heart failure decrease the activity of the vagus nerve, which degrades the function of autonomic nervous regulation of cardiovascular system.
Compared with the healthy group, on the different scales, PDSE entropy of heart failure group were significantly lower (p < 0.05). Because high scale mainly represents low frequency components on time scale, and the low frequency components is mainly associated with the regulation of the body's sympathetic nervous, it explains the occurrence of heart failure, at the same time reduces the activity of sympathetic nerve. With the increase of scale, the vagus nerve weaks, sympathetic nerve function increase. In Figure 7, only in different scales, difference of the heart failure group and healthy group by PDSE, are found reduced in the high scale. This indicate that the occurrence of heart failure on the influence of autonomic nerve may first impact on the vagus nerve, therefore low timescale PDSE value is lower obviously, so it is presented that difference between high heart failure group and healthy group on time scale of PDSE is smaller. Xiao proposed the cardiac contractility variability (CCV) in the study of myocardial systolic function and heart sounds based on amplitude change regularity [13]. Reduction of myocardial systolic function can cause reduction of CCV. This is the same as the conclusions in this paper based on the analysis of first heart sound signal amplitude sequence by PDSE.
Figure 7: Multi-scale analysis error bar chart.
Discrimination two populations with Fisher discriminant method [14], selection of scale on the 1, 2, of PDSE as testing index, respectively to remember as x1 , x2 and the discriminant function is Equation 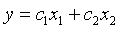(14):
(14)
PDSE value of amplitude sequence of 108 cases of heart failure, 120 cases of healthy first heart sound signal amplitude sequence on 1 and 2 time scale is put into Equation (14), and we get the coefficient of the detection index in the Table 2, the test results are shown in Table 3. Evaluation index including sensitivity (Sen) and specific (Spe). Sensitivity refers to the ratio of diagnosed number of cases in the heart failure group and total heart failure group. Specific refers to the ratio of diagnosed number of cases in health group and total cases of health group. Literature [15] used the symbolic time irreversibility index DE to analyse heart failure based on ECG signal, and sensitivity and specific degree is 93.2%, 94.4%, respectively. In this paper, by contrast, sensitivity and specific degrees are significantly improved, and the diagnosis of discriminant method is simple, easy for clinical application.
| Detection Coefficient | Value |
|---|---|
| C1 | 0.125 |
| C2 | -0.004 |
Table 2: The detection coefficient.
| Sample Size | Evaluation Index | |||
|---|---|---|---|---|
| The results | Heart failure(108) | Healthy(120) | Sen | Spe |
| Heart failure | 105 | 4 | 97.2% | 96.7% |
| Healthy | 3 | 116 | ||
Table 3: Heart failure test results.
Based on the characteristics of heart physiological signal, this paper puts forward a kind of Symbol Entropy Based on Probability Distribution (PDSE) algorithm which is suitable for heart sound signal analysis. This algorithm has realized:
(1) Obtain the symbol sequence can reflect the timing relationships of heart sounds original sequence and can eliminate effect of heart sound original sequence probability distribution to symbolic process;
(2) Break the traditional linear constraint of uniform symbolization, and distribute more symbols in the first heart sound amplitude comparatively dense distribution region, fewer symbols in a relatively sparse area;
(3) Use self-adaption means to decide the size of the symbol set in the process of symbolization.
Obviously, this kind of targeted algorithm, makes the symbol entropy are more sensitive to the change of heart sounds data and can capture nonlinear abnormal state of heart sound signals quickly. Through heart sound simulation experiment of the health and heart failure group, heart failure diagnosis sensitivity and specific evaluation index was respectively 97.2%, 96.7% based on this algorithm, which shows that the algorithm has potential application value of study of heart failure and provides non-destructive diagnosis of heart failure with a new idea.
This work is supported by the National Natural Science Foundation of China (Grant Nos. 61271334).