ISSN: 2320-2459
ISSN: 2320-2459
1Department of Physics, College of Science, UAE University, PO Box 15551, Al-Ain, United Arab Emirates
2Department of Physics, Integral University, Lucknow 226 026, India
Received Date: 23/03/2016; Accepted Date: 06/05/2016; Published Date: 08/05/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Three wave parametric instability of a large amplitude lower hybrid wave in two-ion species plasma is studied analytically. The pump decays into a low frequency mode or quasi mode in the ion cyclotron range of frequency and a lower hybrid wave sideband. The dominant channel of decay is the one for which the low frequency mode is an ion cyclotron wave with frequency close to the ion cyclotron frequency of either ion species. For typical D-T plasma of a tokamak, the growth rate for ω close to deuterium cyclotron frequency, increases with the wave number of the ion cyclotron wave and decreases as the ratio of deuterium to tritium density increases.
Parametric Instabilities; Two-ion species plasma; Lower hybrid wave; Tokamak; Radio frequency heating
Parametric instabilities have been an important feature of large amplitude lower hybrid waves in tokamak as well as smaller plasma devices. During the first decades of nuclear fusion research, high power lower hybrid waves in the 500 MHz-1 GHz frequency range were candidates for heating magnetized plasmas to thermonuclear temperatures. More recently, such waves were found to be mostly attractive at higher frequency (1-5 GHz) for driving non-inductive currents in tokamak plasmas, thus opening the possibility of running tokamak in steady state, and leading to the conceptual design of a steady state tokamak reactor. Radio frequency (RF) heating and current drive of tokamak in the lower hybrid range of frequency has been an active field of research for over three decades. In this frequency range, toroidal plasma current is sustained by replenishing the collisional momentum loss of current carrying suprathermal electrons while ions are heated directly through the Landau damping or via the excitation of parametric instabilities [1-5]. The prominent channels of three wave parametric decay involve an ion-cyclotron mode or quasi mode and a lower hybrid sideband. In the four wave coupling oscillating two stream instability is the most dominant process. Resonant decay into two lower hybrid waves is also a completing process [6-11].
The current drive experiments on a number of tokamak machines have been successfully performed. Fully non inductive discharges of up to 3.6 MA in JT-60U [12], 3 MA in the Joint European Torus (JET) [13] and 0.5 MA during 6 min in Tore Supra [14] have been achieved with lower hybrid waves. The projected ITER lower hybrid systems will inject approximately 50 MW of power and they are optimized for the off-axis current drive functions [15]. Liu et al. have investigated the Lower hybrid wave (LHW) heating in deuterium plasma in the HT-7 tokamak [16]. The ion and electron temperatures were increased by 0.4 keV and 0.3 keV respectively for PLH∼300kW. The ion heating has been observed in the HL-1M tokamak when the plasma density exceeded 3.5 × 1013 cm-3 [17]. LHW experiments have been performed in HT-6M tokamak by Li et al., they have reported the quasi-steady state H-mode with high plasma density by the injection of lower hybrid heating (LHH) and lower hybrid current drive (LHCD) with a power threshold of 50 kW [18]. A good confinement was obtained in ASDEX by combining LHCD and neutral beam injection (NBI) [19]. A full wave current drive with a very high density (4.5 × 1019 m-3) was obtained in the high-field Frascati Tokamak Upgrade (FTU) [20]. Fisch [21,22] has given an elegant review of lower hybrid wave heating and current drive in tokamak. Recently, Ahmad [23] has pointed out the parametric excitation of ion-ion hybrid mode by a lower hybrid wave in D-T plasma where growth is faster for higher deuterium to tritium density ratio.
Observations in space indicate that LH waves are among the most important waves in the earth’s magnetosphere. In fact, LH wave play a central role in the process of collision less energy and momentum transport in space plasmas. Recently there has been much interest [24,25] in magneto sonic and other waves in multi-ion plasmas.
Two ion species plasma in tokamak has the possibility of extra channels of parametric decay. In this paper, we study the parametric decay of a large amplitude lower hybrid wave into an ion cyclotron wave and lower hybrid sideband wave in two ion species plasma such as those considered for nuclear fusion. The channels of decay are: i) resonant decay into an ion cyclotron mode near the ion cyclotron frequency of the either ion species, ii) nonlinear cyclotron damping on either ion species. The lower hybrid pump wave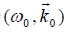 imparts an oscillatory velocity
imparts an oscillatory velocity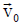 to electrons. The latter beats with the density perturbation due to the low frequency mode
to electrons. The latter beats with the density perturbation due to the low frequency mode 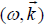 to produce a nonlinear density perturbation, driving the sideband lower hybrid wave
to produce a nonlinear density perturbation, driving the sideband lower hybrid wave 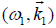 , where
, where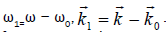 The sideband couples with the pump to produce a ponder motive force on electrons that drive the low frequency mode.
The sideband couples with the pump to produce a ponder motive force on electrons that drive the low frequency mode.
In Sec. 2, we obtain the linear response of electrons to the pump and sideband waves and the low frequency mode. In Section 3, we study the nonlinear coupling and obtain the nonlinear dispersion relation and the growth rate. The results have been discussed in Section 4.
Consider a two-ion species plasma (e.g., tokamak) of equilibrium electron density 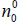 , in a static magnetic field
, in a static magnetic field 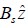 The ion species are characterized by mass m1, m2, density
The ion species are characterized by mass m1, m2, density 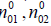 and charge Z1e, Z2e such that
and charge Z1e, Z2e such that 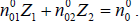 A large amplitude lower hybrid pump wave propagates through the plasma in the x-z plane with electrostatic potential
A large amplitude lower hybrid pump wave propagates through the plasma in the x-z plane with electrostatic potential
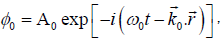 (1)
(1)
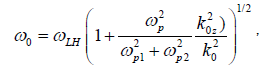 (2)
(2)
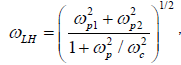 (3)
(3)
where 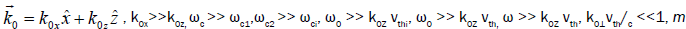 is the mass of electrons,
is the mass of electrons, 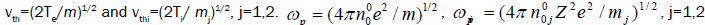 and
and 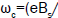
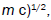 -e and m are the electron charge and mass.
-e and m are the electron charge and mass.
The pump wave imparts oscillatory velocity to electrons 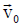 which is governed by the equation of motion
which is governed by the equation of motion
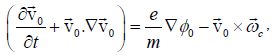
where we have ignored the pressure term. Linearizing this equation and replacing 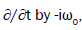
we obtain
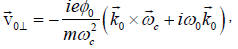 (4)
(4)
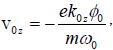 (5)
(5)
Using the velocity perturbation in the linearized equation of continuity
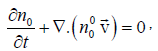
we obtain the density perturbation
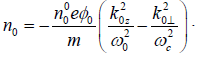 (6)
(6)
The pump wave decays into an electrostatic ion cyclotron mode / quasimode of potential φ and a lower hybrid sideband wave of potential
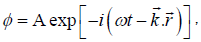 (7)
(7)
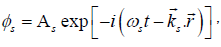 (8)
(8)
where
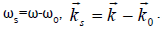
The linear response of electrons to the sideband at 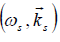 is same as given by Equations (4–5), with
is same as given by Equations (4–5), with 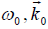 replaced by
replaced by 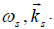
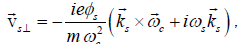 (9)
(9)
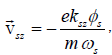 (10)
(10)
The linear density perturbations of electrons and ions at 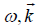 can be written in terms of electron and ion susceptibilities
can be written in terms of electron and ion susceptibilities 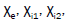
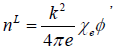
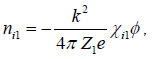
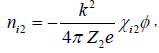 (11)
(11)
where
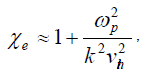 .
.
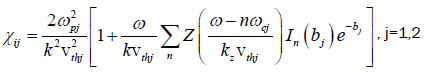
where 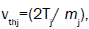 are the ions thermal speeds,
are the ions thermal speeds, 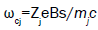 are the ion-cyclotron frequencies
are the ion-cyclotron frequencies 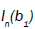 and
and 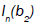 are the modified Bessel functions of order n and arguments b1 and b2, and
are the modified Bessel functions of order n and arguments b1 and b2, and 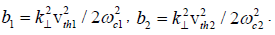
The sideband couples with the pump to produce a low frequency ponder motive force 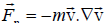 on the electrons.
on the electrons.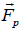 has two components, perpendicular and parallel to the magnetic field. The response of electrons to
has two components, perpendicular and parallel to the magnetic field. The response of electrons to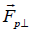 is strongly suppressed by the magnetic field and is usually weak. In the parallel direction, the electrons can effectively respond to
is strongly suppressed by the magnetic field and is usually weak. In the parallel direction, the electrons can effectively respond to 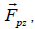 hence, the low frequency nonlinearity arises mainly through
hence, the low frequency nonlinearity arises mainly through 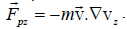
The parallel pondermotive force on electrons at 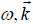 can be written as
can be written as
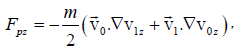
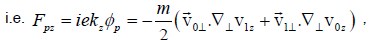 (14)
(14)
The pondermotive potential 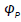 turns out to be
turns out to be
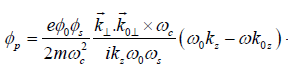 (15)
(15)
The electron density fluctuations in response to 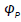 and the self-consistent potential φ at
and the self-consistent potential φ at 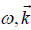 can be written as
can be written as
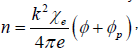 (16)
(16)
The density perturbations of the two-ion species can be written as
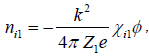
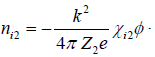 (17)
(17)
Using Eqs. (16) and (17) in the Poisson’s equation
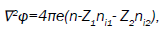
we obtain,
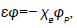 (18)
(18)
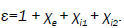
The density perturbation at 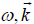 couples with the oscillatory velocity of electrons
couples with the oscillatory velocity of electrons 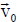 to produce a nonlinear density perturbation at the sideband
to produce a nonlinear density perturbation at the sideband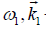 Solving the equation of continuity for the nonlinear density perturbation at the sideband,
Solving the equation of continuity for the nonlinear density perturbation at the sideband,
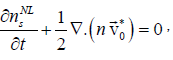
we obtain
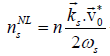 (19)
(19)
The linear density perturbation of electrons due to the self consistent potential 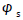
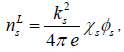 (20)
(20)
The ion density perturbations can be written as
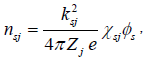 (21)
(21)
where
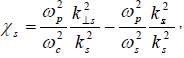
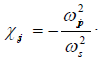
Here we have ignored the nonlinearity arising through ions as it is suppressed by their large mass.
Using these electron and ion density perturbations in the Poisson’s equation
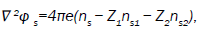
we obtain
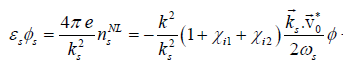 (22)
(22)
Equations (18) and (22) yield the nonlinear dispersion relation
ε ε=μ, (23)
where
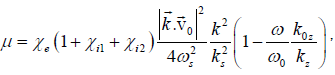 (24)
(24)
We solve Eq. (23) in the case of resonant decay.
In case 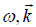 and
and 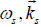 in the absence of the pump, satisfy the linear dispersion relations corresponding to ion cyclotron and lower hybrid waves respectively, the decay process is termed as resonant decay.
in the absence of the pump, satisfy the linear dispersion relations corresponding to ion cyclotron and lower hybrid waves respectively, the decay process is termed as resonant decay.
In the vicinity of 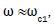 when
when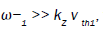 the linear dispersion relation for the low frequency mode (=0) takes the form
the linear dispersion relation for the low frequency mode (=0) takes the form
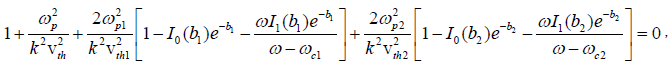
giving
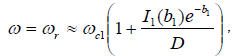 (25)
(25)
where
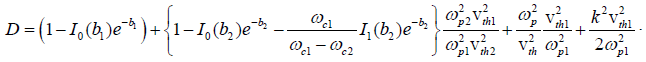
The linear dispersion relation for the sideband 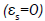 gives
gives
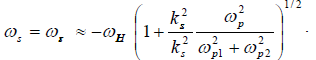 (26)
(26)
In the presence of nonlinear coupling we write
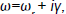
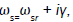
and expand ε and εs around ωr and ωsr as
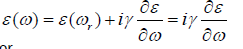
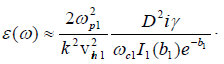 (27)
(27)
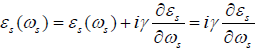
or
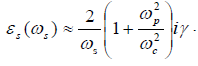 (28)
(28)
where we have suppressed the subscript r on ωr and ωs for the sake of brevity. Then the nonlinear dispersion relation gives
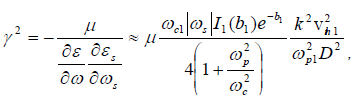 (29)
(29)
Equation (29) simplifies to
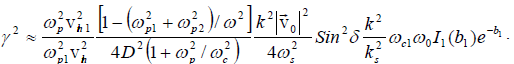 (30)
(30)
where δ is the angle between 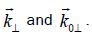
In order to have numerical appreciation of the growth rate, we have carried computations of growth rate for the following parameters: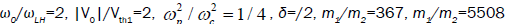 (D-T plasma),
(D-T plasma),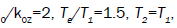
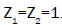 We have plotted in Figure 1, the variation of normalized growth rate,
We have plotted in Figure 1, the variation of normalized growth rate, 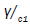 as a function of
as a function of 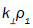 (where
(where 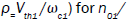
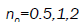
At high power, lower hybrid waves are prone to parametric decay because of their large electrostatic component in the direction perpendicular to the equilibrium magnetic field. This was particularly the case in experiments where the wave frequency was chosen for ion heating through the lower hybrid resonance. A high fraction of the injected power was found to decay nonlinearly into lower frequency daughter waves, and this phenomenon often prevented the power to reach the plasma core and heat the plasma efficiently. At the higher frequencies required for current drive, the question of parametric decay seems to be less severe, but it remains open, especially at high density, and it is the subject of extensive theoretical and experimental investigations. Lower hybrid wave is parametrically unstable when the oscillatory velocity of electrons is of the order or greater than the sound velocity. For tokamak parameters, the powers required are of the order of ≥10 MW. The decay into an ion cyclotron wave and a lower hybrid wave possesses large growth rate. The coupling between high and low frequency modes is provided primarily by the parallel ponder motive force on electrons involving 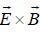 drift.
drift.
For a typical D-T plasma of a tokamak, the growth rate for ion cyclotron wave with frequency ω close to deuterium cyclotron frequency increases with the wave number of the ion cyclotron wave. However, the growth rate decreases as the ratio of deuterium to tritium density increases.