Weakness and Problem in Quantum Field Theory, Which Leads to the Development of the Confined Quantum Field Theory

Quantum Field Theory

Quantum field theory, already from the beginning was suffering from the different problem, weakness, and inconsistency. These problems sometimes cause that some people even questioning the legitimacy of the quantum.

One of the Predominant Problems has been the Divergences

Divergences are the case that we in our calculation get infinities. Physical objects have finite size and value. Then when we deal with physical objects and our calculations lead to an infinite number, something must be wrong. In this case, people try to hide and repair the problem often by pragmatically methods without any physical explanation, like cut-off. The cut-off is that one cut the tail that goes to infinity. The other way to go past the problem is renormalization. In quantum field calculation one start with the main structure or the mother of theory or generating functional this is either Hamiltonian or Lagrangian. Hamiltonian or Lagrangian describe the energy structure of the physical object we deal with. Since energy is the source of the change, Lagrangian or Hamiltonian say how the system will change over time and we can calculate different values in time like cross-sections in scattering and so on. But what happens when we get infinities in these calculations. Infinities are undefined in mathematics. The infinities signal that we do not have legitimate theory. In renormalization people repair the problem in this way. They introduce a parameter in Lagrangian or Hamiltonian. And by driving this parameter to infinity get control over the scattering and get a finite number. In another word to get a finite scattering value which is physically acceptable, they make the mother of the theory, Lagrangian or Hamiltonian undefined. This is not a fundamental solution.

These kinds of problems weakness and paradox oblige us to seek for a stronger base in physics and that is confined quantum field theory.

Special and general relativity are both stronger and physically proved bases in physics. Confined Quantum Field Theory is to extend their moral into the quantum domain.

One of the basic assumptions of the quantum field is that each point of the field posses infinite degrees of freedom. This is, in fact, the main source of the problem.

Let us describe the problem in a very simple way.

Look at these two integrals;

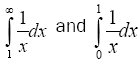
Both are infinite. One has finite integrand but integrated over the infinite domain and the other has bounded domain but the integrand is not bounded. These two types of integral represent what is called in quantum field infrared and ultraviolet divergences. Let see how Confined Quantum Field Theory master this problem in a very fundamental way. What says special relativity? It says that the speeds of physical objects are limited by the speed of light. Therefore an object or part of it cannot in, finite time be infinitely far away. Therefore we do not have the problem of the first kind. What says the moral of the general relativity? It predicts a relation between energy density and the metric of the space. Metric is the distance between the neighbouring points. Therefore in finite energy, the points are bounded to the neighbours by a metric which is a function of energy density and therefore does not have an infinite degree of freedom and consequently the integrand of the second integral must always be finite. And we do not ha ve the other integral problem. Therefore in Confined Quantum Field Theory, we do not have either infrared or ultraviolet divergences. Divergences are not the only problem in quantum. Generally, paradox and uncertainty are not acceptable in physics. People gradually recognize that Confined Quantum Field Theory is a way for more powerful and exact physics and by applying it we can go beyond paradox and uncertainty.