Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Somayeh Nuri*
Department of Electrical Engineering, Urmia Branch, Islamic Azad University, Urmia, Iran
Received date: 21/11/2012 Revised date: 15/12/2012 Accepted date: 27/12/2012
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Despite the generally accepted use of the LSCMA, few analytical results on its convergence have appeared in the open literature. The performance of the algorithm has instead been demonstrated through Monte Carlo simulation. The lack of analytical results is due to the difficulty of analyzing the non-linear CMA cost function. Existing work on the convergence behavior of CMA mostly deals with finding minima of the CMA cost function and finding undesirable stable equilibrium in equalization applications. We next examine an environment containing two complex sinusoids, and show that the LSCMA output SIR can be predicted for each iteration. It is shown that the average behavior of the LSCMA in this environment is similar to the deterministic behavior in the two-sinusoid environment. Finally, an environment containing a CM desired signal and Gaussian interference is examined
Adaptive, Gaussian, Interference, convergence.
A notable exception is the work by Treichler and Larimore on convergence of SGD CMA in an environment containing two complex sinusoids[1,2,3,4,5,6,7,8]. Their work predicts the output power of each sinusoid in a temporal filtering application. The Analytic CMA (ACMA) algorithm presented by van der Veen in should also be noted. This algorithm solves directly for a set of beam former weight vectors that spatially separate a set of CM signals. The ACMA, although effective in many situations, is fairly complex and its behavior with closely spaced and/or low SNR signals is not clear. For these reasons it is recommended in that the ACMA be used to initialize the LSCMA, and that several iterations of the LSCMA be used to find the optimal solutions for the weight vectors. In this paper we determine the convergence rate of the LSCMA in some simple environments, including: (1) high output SIR; (2) sinusoidal desired signal and sinusoidal interferer; (3) CM desired signal and CM interferer; (4) CM desired signal and Gaussian interferer. We assume that the interference is uncorrelated with the desired signal. The convergence rate is expressed in terms of the SIR improvement achieved with one iteration of the LSCMA. The main advantage of CMA is that it is a 'blind' adaptive algorithm, i.e., it does not require a training signal. Other blind adaptive algorithms have been designed to exploit cyclo-stationarity known signal constellation, known spreading code in CDMA, and time or frequency gated properties. The first CMA to be proposed was based on a Stochastic Gradient Descent (SGD) form. The main drawback of this method is its slow convergence. A faster converging CMA similar in form to the Recursive Least Squares method is the orthogonal zed CMA. Another fast converging CMA is the Least Squares CMA (LSCMA), which is a block-update iterative algorithm. It is guaranteed to be stable and is easily implemented. We first examine the situation where the LSCMA output SIR is high We show that if the interference is perfectly removable, each LSCMA iteration will increase the output SIR by approximately 6 dB. This result is valid for any CM desired signal (arbitrary angle modulation), and any uncorrelated interference. We next examine an environment containing two complex sinusoids, and show that the LSCMA output SIR can be predicted for each iteration. The results are analogous to those presented in [3,4,5,6,7]. An environment containing two CM signals, each having random phase, is then considered.
We now examine the behavior of the LSCMA with a CM signal and Gaussian interference. These results are of interest since the distribution of a large number of co-channel interferers, as might be encountered in CDMA applications, will tend toward Gaussian by the central limit theorem. The input to the hard-limiter is expressed as :
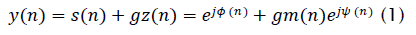
where s(n) is an angle-modulated signal and z(n) is unit-variance complex Gaussian interference. Note that (ψ(n)is uniformly distributed over (- π,π]while m(n) is Rayleigh distributed with PDF:
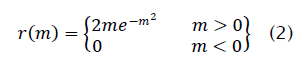
The cross-correlation of s( n) and d( n) is
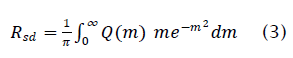
Where,
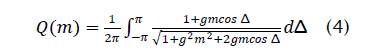
In a similar fashion it can be shown that
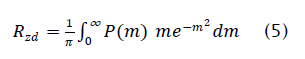
Where,
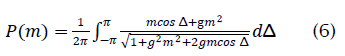
Both (11) and (12) are evaluated by numerical integration and used to obtain the SIR gain shown in Figure 1. The SIR gain as measured from simulations is also shown in Figure 2 and verifies the theoretical analysis. The simulation parameters are the same as those used previously. As before the SIR gain tends to 6 dB as the input SIR becomes high. Note that the SIR gain is greater than 0 dB even for an input SIR of -10 dB. This would seem to indicate that LSCMA can be expected to converge even at low initial input SIR. However, it is important to bear in mind that these results are based on probabilistic notions.
We first examine the situation where the beam-former output SIR is high, as might be the case near LSCMA convergence. We model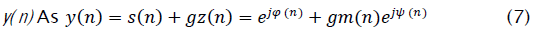 
where φnis the phase of the desired signal s(n), and m(n) and ψ(n) are the magnitude and phase, respectively, of the unit-variance interference term, z(n). The scalar 9 controls the SIR, and we assume gâª1 . Note that we have assumed for convenience that the desired signal has unit amplitude in the beamformer output. This has no effect on the behavior of the LSCMA, since any scaling of y(n) is removed by hard-limiting The cross-correlation of s( n) and d( n) is
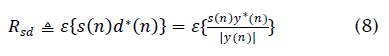
Using the binomial approximation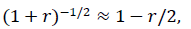 
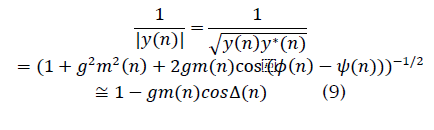
where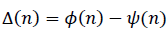 
Before proceeding further we consider the PDF of Δ(n) . We are concerned here with the PDF of the phase difference of two independent complex baseband signals for the case in which the PDF of the phase of each signal is uniform over (-π,π]. The desired PDF is obtained by convolving two uniform PDFs, which results in a triangular-shaped PDF over (−2π,2π]. Since the phase wraps 
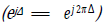the PDF of Δ is uniform over (−π,π]. This is true even if the received signals have the same modulation format and identical carrier frequencies. The cross-correlation of s( n) and d( n) can now be approximated as
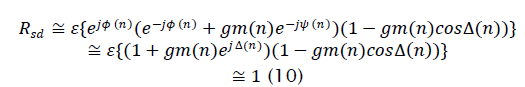
where the magnitude of the interfering signal m( n) and the phase difference ~(n) are assumed independent. The result that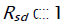 
is intuitively appealing since the SIR is high.
The cross-correlation of z( n) and d( n) is
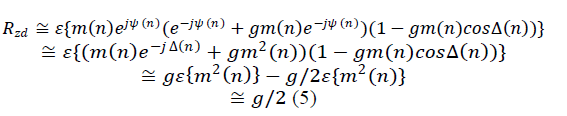
The output SIR (22) now becomes
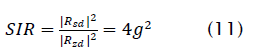
Since the input SIR is 1/ g2, the ratio of the output SIR to the input SIR is 4, so that the SIR increases by 6 dB. This result for high SIR holds for any CM signal with uncorrelated cochannel noise and interference and will be observed in the simulation results to follows.
Background Noise Inclusion
In this section we examine the effect of background noise on the behavior of the LSCMA. We assume that the noise has a complex circularly symmetric Gaussian distribution and is uncorrelated from sensor to sensor. We consider one environment where the interference is Gaussian, and another where the interference is CM. In both cases the desired signal is QPSK and is assumed to have been match filtered and sampled so that it is CM. All simulation results are based on 1000 trials with the LSCMA block size equal to 256 symbols. The array is linear with eight elements and uniform interelement spacing equal to ��/2. The signal power is measured relative to the unit variance background noise, and is termed the Signal to White Noise Ratio (SWNR).
Figure 1: Improvement in output SIR achieved with one iteration of LSCMA with a QPSK desired signal received with a Gaussian interferer and Gaussian background noise. Solid lines indicate theoretical result, '+','0', and 'x' denote mean gain from simulation.
First consider the case where the desired signal is incident from 0° and a single Gaussian interferer is incident from 5°. Since the noise and interference is Gaussian, the SINR gain from hard-limiting is given by (57) and (59). The LSCMA output SINR is related to the SINR gain from hard-limiting by (34). The mean LSCMA SINR gain is presented in Figure 1 for SWNR equal to 5, 10, and 20 dB. The power of the interferer is kept equal to the power of the desired signal. The figure shows excellent agreement between the measured and predicted SINR gain. As the SWNR increases, the optimal output SINR increases, and the SINR gain approaches the gain obtained when no background noise is present. Now consider the case where the interference is CM. Since the interference is not Gaussian, calculation of the SINR gain is tedious and it is appropriate to make some approximations. When the beamformer output SINR is low, the dominant source of distortion is the CM interferer, and the SIR gain from hard-limiting can be accurately predicted by the results for CM interference, given by (53) and (54). As the output SINR becomes higher, the interferer is nulled, and the background noise becomes the dominant source of distortion. However, we have shown that in all cases the SINR gain from hard-limiting approaches 6 dB as the SINR becomes high. Therefore the behavior of LSCMA in this case can be predicted by using the results for CM interference (53) and (54) together with (34). Simulation results for an environment similar to that described above, except that the Gaussian interferer is replaced with a CM QPSK interferer, are presented in Figure 2. This figure shows very good agreement between the approximate theoretical result and the simulation results.
Figure 2: Improvement in output SIR achieved with one iteration of LSCMA with a QPSK desired signal received with a QPSK interferer and Gaussian background noise. Solid lines indicate theoretical result, '+','0', and 'x' denote mean gain from simulation.
The results presented here can form a basis for analysis of these multi-signal extraction techniques. Clearly the variance and distribution of output SINR obtained with the LSCMA is also an important area for investigation. We finally comment on the hard-limit non-linearity. For high SIR, the hard-limiter is the optimal non-linearity when the desired signal has a constant envelope. However, at low SIR other non-linearities can yield greater SIR gain. Thus it is possible that non-linear functions other than the hard-limit can be used to develop blind adaptive algorithms which converge faster for low initial SINR.