Cylindrical Shock Waves in a Low Conducting Gas in Presence of Axial and Azimuthal Components of Magnetic Induction

Abstract

The propagation of diverging cylindrical shock waves in a low conducting gas under the influence of spatially variable axial and azimuthal components of magnetic induction, by using the method of self-similarity. The initial density of the medium is assumed either to be uniform or to obey a power law. Also, both the components of the initial magnetic induction are taken to vary as some power of the distance from the axis of symmetry. The total energy of the flow-field behind the shock is constant or increasing due to instantaneous or time dependent energy input. The effects of variation of the initial density and the ratio of specific heats of the gas, on the propagation of shock and the flow-field behind it are investigated.

Keywords and Phrases

Shock waves, self-similar flow, variable initial density, variable initial magnetic induction, variable energy input, low electrical conductivity.

Introduction

Lin [1] has extended the Taylor’s analysis [2] of the intense spherical explosion to the cylindrical case. The law of variation of the radius of a strong cylindrical shock wave produced by a sudden release of a finite amount of energy was obtained. Applying the results of this analysis to the case of hypersonic flight, it was shown that the shock envelope behind a meteor or a high speed missile is approximately a paraboloid.

Since at high temperatures that prevail in the problems associated with shock waves a gas is ionized, electromagnetic effects may also be significant. A complete analysis of such a problem should therefore consist of the study of the gasdynamic flow and the electromagnetic field simultaneously. The study of the propagation of cylindrical shock waves in a conducting gas in presence of an axial or azimuthal magnetic induction is relevant to the experiments on pinch effect, exploding wires and so forth. This problem both in the uniform or non-uniform ideal gas was undertaken by many investigators, for example, Pai [3], Cole and Greifinger [4], Sakurai [5], Bhutani [6], Christer and Helliwell [7], Deb Ray [8], Vishwakarma and Yadav [9]. One of the basis assumptions of these works is that the shock wave is propagated in a gaseous medium as a result of an instantaneous release of energy along a line.

While the assumption of instantaneous energy input is considered adequate for most problems, there are processes in which the energy input, though very rapid, can be considered to be time dependent. Examples of time dependent energy input are the arc discharges, exploding wire phenomena and chemical energy release (as might occur in two phase detonations). Freeman [10] has considered the propagation of shock waves resulting from variable energy input. He has paid special attention to the case of cylindrical symmetry in view of its particular application to the problem of cylindrical spark channel formation from exploding wires (Freeman and Craggs [11]).

In the present work, we studied the propagation of diverging cylindrical shock waves in a low conducting and uniform or non-uniform gas as a result of time dependent energy input, under the influence of spatially variable axial and azimuthal components of magnetic induction. The medium ahead and behind the shock front are assumed to be an inviscid one and to behave as a thermally perfect gas. The initial density of the gas is assumed to be uniform or to vary as some power of distance. The total energy of the flow-field behind the shock is not constant, but increasing due to time dependent energy input. The gas ahead of the shock is assumed to be at rest. Effects of viscosity, heat-conduction, radiation and gravitation are not taken into account. Distribution of the flow variables between the shock front and the inner expanding surface are obtained, and the effects of the variation of initial density and the ratio of specific heats are investigated.

Fundamental Equations and Boundary Conditions

The basic equations governing the unsteady and cylindrically symmetric motion of a low conducting gas in presence of axial and azimuthal components of magnetic induction are given by (Tyl [12], Sakurai [5] and Vishwakarma [13])

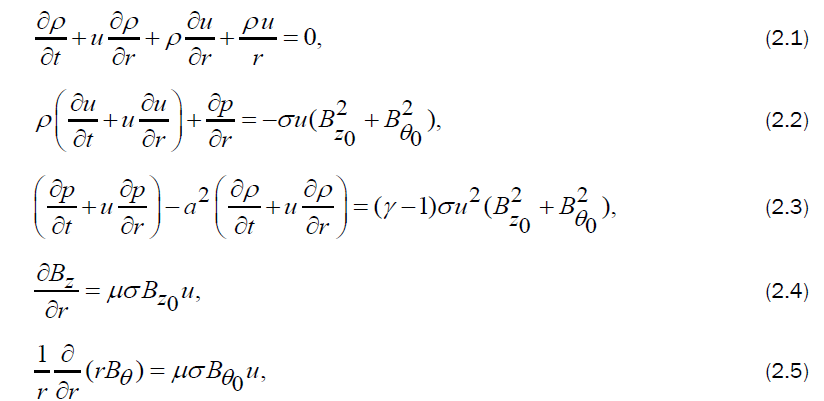
where 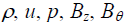are the density, velocity, pressure, axial magnetic induction and azimuthal magnetic induction, respectively, at distance r from the axis of symmetry and at the time t, 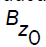is the initial axial magnetic induction, 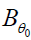the initial azimuthal magnetic induction, γ the ratio of specific heats, μ the magnetic permeability, σ the electrical conductivity and ‘a’ the speed of sound given by

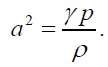
The internal energy per unit mass of the gas e is given by

It is assumed that, due to explosion along the axis of symmetry, a cylindrical shock is produced and propagates into the low conducting gas of density 0 in presence of the axial magnetic induction 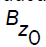and azimuthal magnetic induction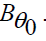

The density of the gas and the axial and azimuthal components of magnetic induction ahead of the shock are assumed to be varying and obeying the laws:

where R is the shock radius and A, α, S, Q, m, n are constants.

Since σ is small, the magnetic induction may be taken continuous across the shock front (Sakurai [5]). Neglecting the counter pressure, the shock conditions may be written as

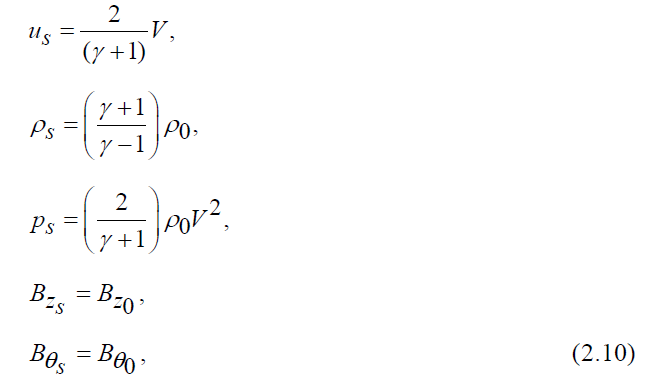
where the subscript s refers the conditions immediately behind the shock front and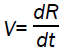 denotes the velocity of the shock.

Similarity Transformations

To obtain similarity solutions, we write the unknown variables in the following form (Vishwakarma and Yadav [9])

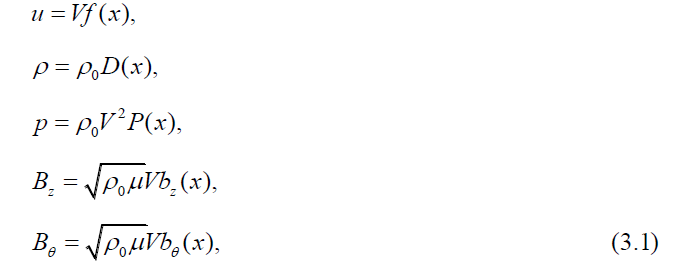
where f, D, P, b_z, and b are the functions of the non-dimensional variable 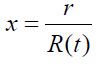only. The shock front is represented by x = 1.

The total energy of the flow-field behind the shock is not constant, but assumed to be time dependent and varying as (Rogers [14], Freeman [10], Director and Dabora [15]).

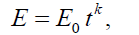            (3.2)

where E₀ and k are constants. The positive values of k corresponds to the class in which the total energy increases with time. Since the flow is adiabatic and the shock is strong, this increase can only be achieved by the pressure exerted on the fluid by an expanding surface (a contact surface or a piston). The situation very much of the same kind may prevail in the formation of cylindrical spark channel from exploding wires. In addition, in usual cases of spark breakdown, time dependent energy input is a more realistic assumption than instantaneous energy input (Freeman [10]).

The total energy of the flow between the shock front and the inner expanding surface (piston) is therefore expressed as

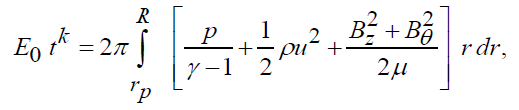         (3.3)

where r_p is the radius of the inner surface.

Applying the similarity transformations (3.1) in the relation (3.3), we find that the motion of the shock front is given by the equation

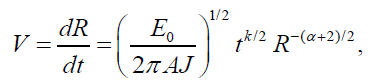            (3.4)

where

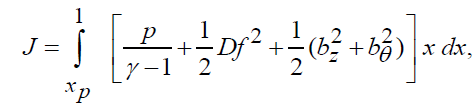
x_pbeing the value of the x at the inner expanding surface.

Equation (3.4), on integration, yields

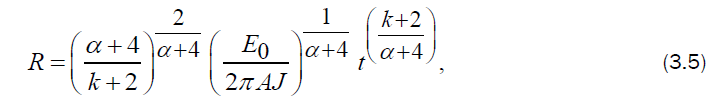
and therefore,

After using the similarity transformations, the equations (2.1) to (2.5) change into the following set of ordinary differential equations

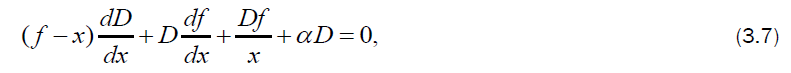
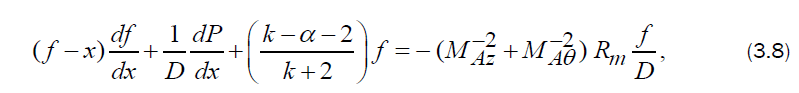
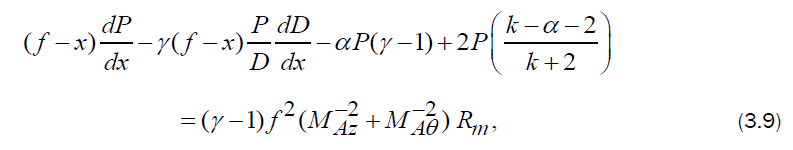
where 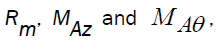are respectively, the magnetic Reynolds number, axial Alfven-Mach number and azimuthal Alfven-Mach number, and they are given by

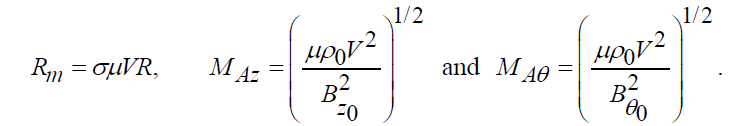
Using the self-similarity transformations (3.1), the boundary conditions (2.10) can be written as

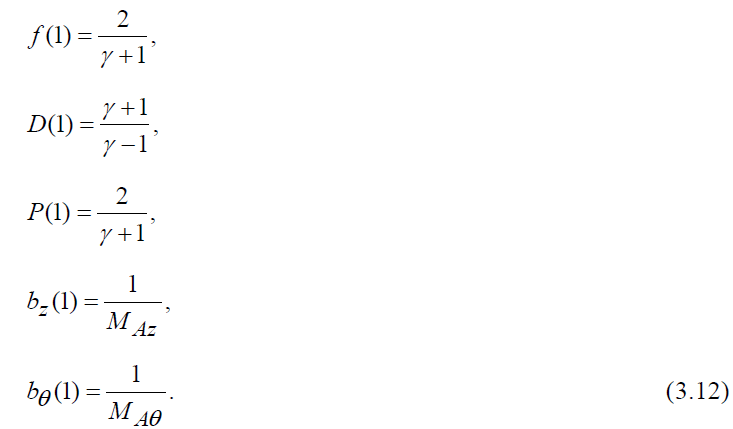
For the existance of similarity solutions magnetic Reynolds number R_m, axial Alfven-Mach number M_Az and azimuthal Alfven-Mach number M_{A} should be constants. Therefore,

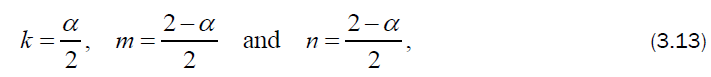where

By solving equations (3.7) to (3.9) for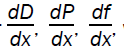 we get

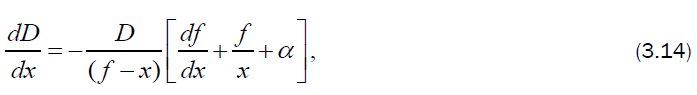
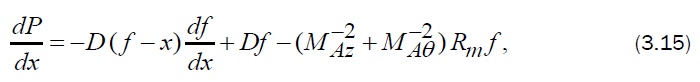
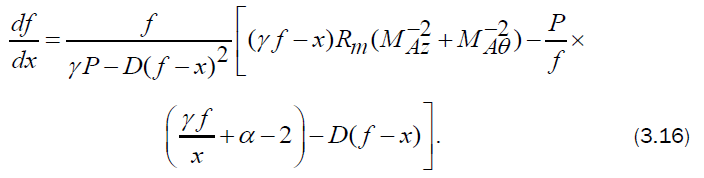
The condition to be satisfied at the inner expanding surface is that the velocity of the fluid is equal to the velocity of the surface itself. This kinematic condition, can be written as

For exhibiting the numerical solutions it is convenient to write field variables in the following form:

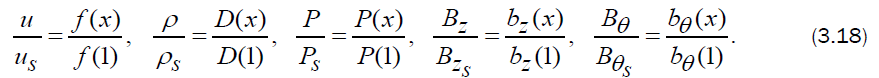
The shock-boundary conditions in terms of these variables are

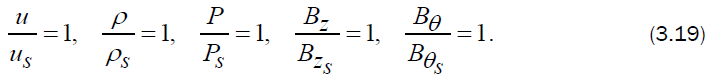
Now, the differential equations (3.10), (3.11) and (3.14) to (3.16) may be numerically integrated, with the boundary conditions (3.12) to obtain the flow-field between the shock front and the inner expanding surface.

Results and Discussions

The reduced flow variables 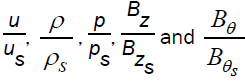are obtained by numerical integration of the differential equations (3.10), (3.11) and (3.14) to (3.16) with the boundary conditions (3.12). For the purpose of numerical integration, the values of the constant parameters are taken as (Vishwakarma and Singh [16]) γ = 1.4,1.66; 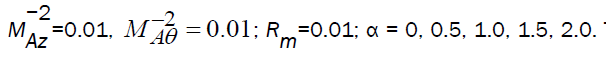The value α = 0 corresponds to the case of shock wave generated by instantaneous energy release (k = 0) in a gas of uniform density.

Figures 1-5 show the variation of the flow variables 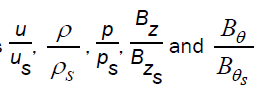with x at various values of the parameters α and γ. It is shown that, as we move inward from the shock front towards the inner expanding surface, the reduced fluid velocity 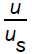decreases for lower values of α (= 0,0.5), but it increases for comparatively higher values of α (= 1.5, 2.0); and the reduced density 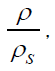reduced pressure 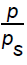and reduced axial magnetic induction 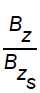decrease for all acceptable values of α, whereas reduced azimuthal magnetic induction 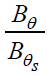increases. Table 1 shows the dimensionless position of the inner expanding surface x_p at different values of α and γ.

The effects of an increase in the density variation index α are (from figures 1-5):

(i) to increase the velocity 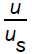and the pressure 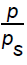at any point in the flow-field behind the shock;

(ii) to decrease the density 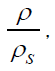and the axial magnetic induction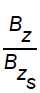

(iii) to decrease the slope of profiles of velocity and pressure and to increase that of the profiles of the density and axial magnetic induction; and

(iv) to decrease the distance (1−x_p) of the inner expanding surface from the shock front (see table 1). This means that the ratio of the velocity of inner expanding surface to that of the shock front increases which results in more compression of gas behind the shock and an increases in the shock strength.

In fact, by an increase in α, k is increased which increases the time dependent energy input (through equation (3.2)) causing an increase in the velocity of inner expanding surface and hence an increase in the shock strength. The effects of an increase in the γ are (from figures 1-5):

(i) to decrease the velocity 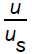and to increase the density 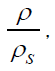and the axial magnetic induction 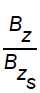at any point in the flow-field behind the shock;

(ii) to decrease the slope of profiles of density and axial magnetic induction; and

(iii) to increase slightly the distance of inner expanding surface to the shock front (table 1).

Variation in α or γ has no effect on the azimuthal magnetic field 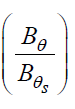in the flow-field behind the shock.

Equations (3.5) and (3.13) show that the shock velocity ̇R decreases with time and varies as t^−1/2.

Table 1. Position of the inner expanding surface x_p at different values of α and γ for and R_m=0.01.

Figure 1.

Figure 2.

Figure 3.

Figure 4.

Figure 5.

Conclusions

In the present paper, the similarity solutions have been obtained for the propagation of cylindrical shock waves in a low conducting gas under the influence of variable initial axial and azimuthal components of magnetic induction. On the basis of the present study, one may draw the following conclusions:

(i) The shock velocity decreases with time as t^−1/2.

(ii) An increase in the value of density variation index α gives rise an increase in the velocity 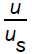and in the pressure 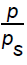, and a decrease in the density 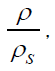and in the axial magnetic induction 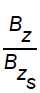at any point in the flow-field behind the shock.

(iii) An increase in α, increases the time dependent energy input, and hence increases the shock strength.

iv) An increase in the value of γ gives rise an increase in the density 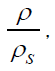and in the axial magnetic induction 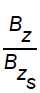,and a decrease in the velocity 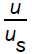at any point in the flow-field behind the shock.

References

1. Lin SC, Cylindrical shock waves produced by instantaneous energy release. J Appl Phys. 1954;25:54-7.
2. Taylor G, The formation of a blast wave by a very intense explosion. Proc Royal Soc Lond A. 1950;201:159- 74.
3. Pai SI, Cylindrical shock waves produced by instantaneous energy release in magnetogasdynamics. Proc Theo Appl Mech. 1958;81:89-00.
4. Cole JD, Greifinger C, Similarity solution for cylindrical magnetohydrodynamic blast waves. Phys Fluids.1962;5:1597-7.
5. Sakurai A, Blast wave theory. Basic Developments in Fluid Dynamics. Vol. 1 (Ed. M. Holt), Academic Press, New York. 1965;309.
6. Bhutani OP, Propagation and attenuation of a cylindrical blast wave in magnetogasdynamics. J Math Anal Appl. 1966;13:565-76.
7. Christer AH, Helliwell JB, Cylindrical shock and detonation waves in magnetogasdynamics. J Fluid Mech. 1969;39:705-725.
8. Deb Ray G, Similarity solutions for cylindrical blast waves in magnetogasdynamics. Phys Fluids. 1973;16:559-560.
9. Vishwakarma JP, Yadav AK, Self-similar analytical solutions for blast waves in inhomogeneous atmospheres with frozen-in-magnetic field. Eur Phys J B. 2003;34:247-53.
10. Freeman RA, Variable energy blast waves. Brit. J Appl Phys (J. Phys. D). 1968;1:1697-710.
11. Freeman RA, Craggs JD, Problem of spark channel formations. Brit. J. Appl. Phys. (J. Phys. D). 1969;2:421- 427.
12. Tyl J, The influence of the action of magnetic field on the phenomenon of implosion of a cylindrical shock wave in gas. J Tech Phys. 1992;33:205-218.
13. Vishwakarma JP, Current Trends in Industrial and Applied Mathematics, (Eds. P. Manchanda, K. Ahmad and A. H. Siddiqui). Anamaya Publishers, New Delhi. 2002;109-122.
14. Rogers MH, Similarity flows behind strong shock waves. Quart J Mech Appl Math. 1958;11:411-422.
15. Director MN, Dabora, EK, An experimental investigation of variable energy blast waves. Acta Astronautica. 1977;4:391-407.
16. Vishwakarma JP, Singh AK. Self-similar solutions for cylindrical shock waves in a low conducting gas. Aligarh Bull Maths. 2009;28:5-14.