Review of the Substance Structure Theory and its Application of Wave Elements

Abstract

Existing theories of material structure and quantum field theory cannot describe the specific sources of fundamental particles. In quantum field theory, the generation of particles is the instantaneous transformation of the field, rather than the true creation of particles. It is necessary to explore the composition (or source) of the next level of elementary particles or fields. The material structure theory of "all fundamental particles mainly originate from photons" has great advantages in combining logic and fact. By utilizing this new theory of material structure, quantum theory, Bohr theory and classical electromagnetic theory can be mixed to describe the same particle. Both this new theory of material structure and its application examples demonstrate that there is no longer a gap between the micro world and the macro world in calculating the spin angular momentum of basic particles, atomic ionization energy and molecular dissociation energy.

Keywords

Theory of material structure of wave elements; Light-knot electronic structure model; Electron spin magnetic moment operator; Quantum mechanics; Compatibility between quantum mechanics and classical electromagnetic

Introduction

Research progress in material structure theory and its applications

Some people are very satisfied with the existing theories of quantum mechanics and corresponding material structures (especially elementary particle structures), while others are very dissatisfied. For example, many people are dissatisfied with the explanatory system of quantum mechanics. Because that violates local realism and determinism. And this explanatory system has a significant impact on the mathematical form system and applications of quantum mechanics. In chemistry, the application of quantum mechanics is not very accurate. However, conservative people believe that quantitative calculations in quantum chemistry are accurate and successful. Radical people believe that the so-called "accuracy and success" of quantum chemistry calculations are obtained through semi empirical computational programs that are constantly compared with experimental results. Accurately calculating a very simple hydrogen molecule by hand using quantum mechanics cannot be achieved and computer programs are needed. However, the computer program for calculating hydrogen molecules is not solely based on logic, but is mainly woven based on experience and continuous comparison and correction with known experimental values. The quantum mechanical calculations of electron spin angular momentum and spin magnetic moment are consistent with experimental facts. Satisfied people believe that this fact is rigorously calculated, indicating that quantum mechanics is successful and practical. Dissatisfied people believe that we do not know the specific way electrons spin, yet we calculate the physical quantities related to spin motion. From the perspective of formal logic, this is unreasonable. It makes people feel that the calculation results are patchwork, opportunistic, or it seems that there is help from God. It is inevitable to feel that quantum mechanics computing theory is a rootless tree, a skyscraper without a foundation. Even for the calculation of the simplest molecule-hydrogen molecule, the situation is the same: Without knowing the specific structure of hydrogen molecule and the specific motion state and mode of electrons outside the nucleus, the energy eigenvalue of hydrogen molecule (and other physical quantities related to the structure of hydrogen molecule and the motion mode of electrons inside it) is abtained by mechanical calculation. It's also difficult not to experience the negative feelings mentioned above. What is the internal structure of electronics? How is the motion of extranuclear electrons? What is the way electrons spin? These cannot be understood through theories related to quantum mechanics or material structure theory (it is unknown what the electron spin magnetic moment comes from). Physicists do not know the specific motion and complete internal structure of particles, but they have calculated the values of some physical quantities related to the structure and motion of particles. In physics, the existence of things that one wants to know but cannot know is a manifestation of the inadequacy of physical theories. This is the dark cloud over physics, how can we tolerate its existence and easily generate a sense of satisfaction? When you don't know how someone arrived in Guangzhou from Beijing (you only know that he spent 5 days), you cannot calculate the transportation or total cost of their trip. This is normal and in line with formal logic. On the contrary, 'you calculated all the expenses for his trip very accurately' is not in line with formal logic. There is no sufficient reason to believe that quantum mechanics calculations are an exception.

'Very satisfied with the existing physics theory' seems to indicate that people's demands are too low. The author of this article belongs to a group of people who are dissatisfied with existing physics theories. Therefore, long-term exploration of the composition and structure of electrons, intrinsic motion modes (especially the specific way electrons spin), and the motion modes of electrons outside the nucleus.

Many people have also done or are currently doing this kind of exploratory work. The situation I understand is that the vast majority of people have not broken free from the constraints of the concept of point particle structure (including small ball material structure). Therefore, none of them were successful. I want to try to establish new ideas and concepts of material structure in order to dispel the dark clouds over physics.

After long-term efforts, I proposed the wave element particle structure hypothesis (formerly known as the photo junction electronic structure model. This breaks free from the constraints of old physical structure concepts). This particle structure theory can at least explain the specific way electrons spin and the motion of electrons outside the nucleus and accurate quantitative calculations of electron spin momentum and spin magnetic moment may be possible. The integration of the wave element particle structure model into the mathematical formal system of quantum mechanics has brought existing quantum mechanics into the realm of local realism [1-4]. Fortunately, the preliminary applications of wave element particle structure theory and local realism quantum mechanics methods have been quite successful. Anyway, the research work introduced in this article belongs to theoretical iterative creative work. In the field of physics, there has been no research work of this type for over a hundred years. The research work introduced in this article is at least worth discussing and exchanging.

Literature Review

The basic premise of the electronic structure theory of wave elements

Scholars engaged in particle physics research know that high-energy photons can decay into electron anti electron pairs. How to explain this process? The statement of quantum field theory is that "the light field undergoes a process similar to jumping, which turns the light field into an electrostatic field of electrons". Due to the unknown nature of the jumping process, quantum field theory has not yet clarified how photons become electrons, nor has it elucidated the internal structure of electrons, nor dispelled the dark clouds over physics. Today, many people believe that complexity is the right thing to do. However, things that are "simple and beautiful" may also be correct. We cannot rule out this possibility. If we describe the process of photon decay into electrons in the simplest way, that is, photons traveling in a straight line travel along a small circle instead and discrete waves can become things that look like particles. Therefore, it can be assumed that a high-energy photon first decomposes into left-handed circularly polarized photons and right-handed circularly polarized photons and then the left and right circularly polarized photons are connected end-to-end and propagate along a small circle to form electrons and anti-electrons. For convenience, we refer to it as basic assumption. Simply put, this is the light knot hypothesis. Simply put, this is the light-knot hypothesis and also the optical knot electronic structure model. It is not difficult to observe that such a free electron entity is circular (It is a circular phase trajectory�??Phase trajectory ring) and for convenience, this ring can be referred to as an electronic ring. The composite circularly polarized light synthesized by two plane polarized photons can be further decomposed into two plane polarized light. Basic circularly polarized light is non synthetic circularly polarized light that can no longer be decomposed.

Basic assumption 2: The electron ring surrounded by circularly polarized photons can expand its radius (including transition processes) in a quantized form in the central force field, following the rule of rd=274n2r0, (n=1, 2, 3,�??�??�??). When Z=1 (the number of nuclear charges sensed by electrons is 1), r0=λ/2�?=ħ/2mc. The physical quantity with subscript d is the physical quantity of wave particle duality particles described by de Broglie waves. If the bound state particle happens to be an electron, then, r0 is re and md is me. When it is indicated that the described particle is an electron, the subscript in me can be omitted. Basic assumption 3 is about the assumption that two electrons with opposite spin pairs coincide. In atoms and molecules, electron pairing refers to the complete coincidence of two electrons with opposite spin.

The light-knot electronic structure model indicates that photons (i.e., electromagnetic waves) are one of the components or sources of fundamental particles at the next level. Adhering to the principle that entities without static mass are more fundamental than entities with static mass, we assume based on experimental facts that neutrinos are also a component of fundamental particles [5]. In this way, the next level of origin for the composition of elementary particles is photons and neutrinos. The corresponding material structure theory is also known as the theory of wave elements material structure.

Using a photo junction electronic structure model to solve the problem of the source of electron spin magnetic moment

The wave equation frequently used in quantum mechanics is

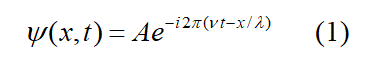
The plane wave solution of the electromagnetic wave equation is similar to it. In the formula, p=2mc=h/λ, E=hν=2mc2, c=λν (This is the commonly used first set of data). According to basic assumption 1 (model of photonic electronic structure), it can be inferred that the energy, momentum and maximum amplitude of photons in circularly polarized light are only half of those in plane polarized light before decomposition. But the frequency, wavelength and propagation speed of the two are equal. Equation (1) is equivalent to (x, t)=Ae-i(Et-xp)/ħ. If it is the basic circularly polarized light decomposed from plane polarized light, during the decomposition process, the frequency and wavelength remain unchanged, but the maximum amplitude is reduced by half. If the wave function of this wave is represented by the functions of ν and λ, the form is still the same as equation (1). Quantitatively, A, E and p are only half of equation (1). Use the second set of data to distinguish when using. The second set of data is p=mc=h/2λ, E=hν/2=mc2, c=λν, λ=2�?r. If describing de Broglie waves, the wave function used is different from the form mentioned above.

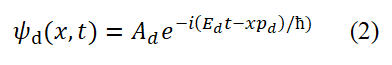
Here, pd=m�?d=h/λd, Ed=hνd=(1/2)m�?d2, �?d=λdνd=αc, λd=2�?rd, λd=2�?rd (This is the third set of data). In this case, Ed no longer contains stationary mass but only kinetic energy Ek or T. Eauation (2) and basic assumption 1 tell us the specific form of spin of free electrons-Basic circularly polarized photons propagate along a small circle-The circular motion of momentum and energy (mass equivalent to energy).

According to assumptions (1) and (2), it can be inferred that when a circularly polarized photon propagates end-to-end along a small circle with a radius of r, there is a relationship of λ=2�?r (using the second set of data). The spin angular momentum of a free electron is the intrinsic angular momentum of the electron's motion, expressed as L =r �?p (via the classical electrodynamics equation). Substituting λ=2�?r, p=mc, ħ=h/2�? into this classical angular momentum expression yields

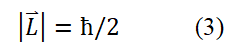
T The method for determining the sign of spin angular momentum in a horizontal circular plane is as follows: When the fundamental circularly polarized photon propagates clockwise, it is defined as negative and counterclockwise, it is defined as positive and the direction perpendicular to the circular plane and above is defined as the positive Z-axis direction. In this case, flipping the circle (or electronic ring) 180° allows the electron spin angular momentum to transition between positive and negative values: L=+ħ/2 and L=-ħ/2. The electron spin angular momentum can be combined and written as L=± ħ/2. According to classical electrodynamics, if the electron spin angular momentum takes a negative value, the relationship between the electron spin magnetic moment and the electron spin angular momentum is

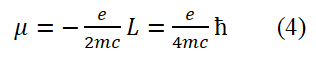
We have elucidated the source of electron spin magnetic moment (i.e., clarified the specific way of electron spin). Knowing the specific way of electron spin motion (which is also its intrinsic motion and structure). Below, we derive the electron spin angular momentum operator and electron spin magnetic moment operator based on basic assumption 1. Calculate the second-order number of layers for x using equation (1) and use the first set of data describing free electrons or bosons to obtain

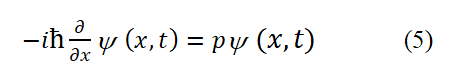
The electron spin angular momentum operator is

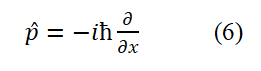
Taking the sign of L in equation (4) as negative, μ=-e/2mc L=e/4mc ħ and substituting the non vector form of equation (3) into it, considering r=λ/2�?=(h/2mc)/2�?=�?/2mc), we obtain

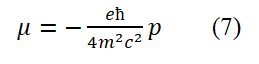
By replacing p in equation (7) with the momentum operator in equation (6), we obtain

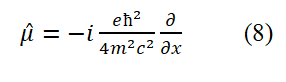
Dividing both sides of equation (8) by (-e/2mc) yields the intrinsic motion (spin motion) angular momentum operator for free electrons

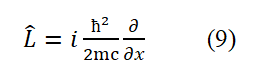
Equation (9) can also be obtained by using the following methods: Replace r in L =r �?p with �?/2mc and replace p with equation (6).

For describing bound state particles or de Broglie waves (Taking the ground state hydrogen atom as an example), we choose the data set of Ed=hνd=1/2 m�?d2, pd=m�?d, �?d=αc, λd=h/pd=h/(m�?d)=2�?rd, Ad, �?d(x,t) (the third set of data) and equation (2). Here, �?d is the group velocity, not the phase velocity.

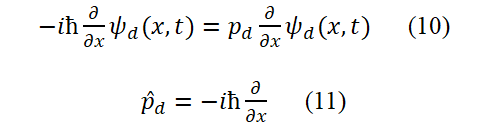
The angular momentum of the orbital motion of bound state electrons is

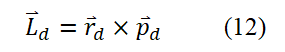
Here, rd=λd/2�?=ħ/pd. Substitute λd=2�?rd�?pd=md�?d�?ħ=h/2�? into equation (12) and use its non vector form to obtain equation (13).

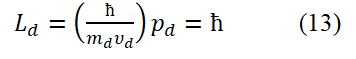
As long as the electronic ring is flipped over, Ld will change its symbol.

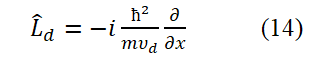
Here, the spin angular momentum in equation (14) has been chosen as a negative value. Substitute equation (14) into equation (7) (i.e., replace p-ud in equation (7) with an operator form in equation (14)),

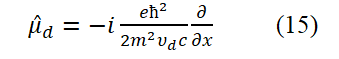
Apply equation (15) to equation (10), we can obtain

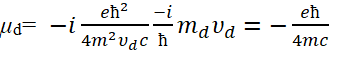
Let's take the ground state hydrogen atom as an example. According to basic assumptions 1 and 2, it can be inferred that in hydrogen atoms, the motion of bound electrons is the orbital motion of electrons and the velocity of bound electrons is �?=αc. Ld and μd are the angular momentum and magnetic moment of electrons in orbital motion, respectively. In this way, the magnetogyric ratio of electron spin motion and the magnetogyric ratio of orbital motion are, respectively.

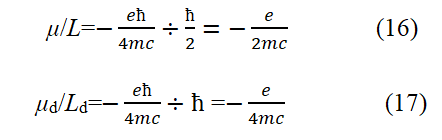
Comparing equations (16) and (17), it can be seen that for the ground state hydrogen atom, the magnetic spin ratio of the intrinsic motion of the electron is twice that of the orbital motion of the electron.

Establish the Schrödinger equation based on basic assumptions 1 and 2 (electronic structure model and hydrogen atom model)

Equation (11) is the momentum operator for bound state electrons. The momentum operator in the form of second-order partial derivatives is

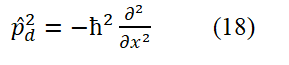
In an electrodynamic equilibrium system, Viry's theorem holds and there is a clear relationship between the kinetic energy and potential energy of particles. For the ground state hydrogen atom, this relationship is

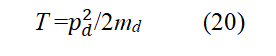
Convert p 2 d in Eq. (20) to operator form

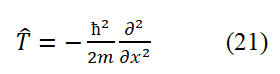
T+V=H is the sum of the kinetic and potential energies of particles in an electrodynamic equilibrium system, excluding the internal energy of the system. Add V to both sides of the above equation. Then, based on the definition of the operator, we can obtain

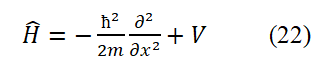
Equation (22) is the Hamiltonian operator. Applying it to the wave function yields the energy eigenvalue H.

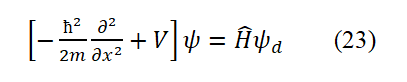
Equation (23) is also the non-relativistic Schrödinger equation. Where, �? is the wave equation for plane polarized light (where E=hν, p=h/λ). Equation (23) corresponds to the energy summation formula T+V=H. Eq.(23) is a non relativistic Schrödinger equation. Among them, �? is the wave equation of plane polarized light (For the 1s electron in the ground state hydrogen atom,

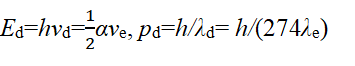
Electron radius, atomic radius, and hydrogen atomic structure model

According to hypothesis 2, it can be inferred that when a small ring of free electrons becomes an extranuclear electron of a hydrogen atom, it undergoes the Huygens iteration process to become a large ring. That is to say, the radius of a 1s electron is 274 times that of a free electron. In this way, the structure of the ground state hydrogen atom is that the hydrogen nucleus is located at the center of a circle surrounded by 274 secondary waves [6]. The radius of this large ring is the radius of the hydrogen atom, also known as the Bohr radius.

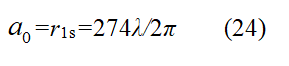
Here, λ is the radius of the free electron, sometimes written as λe. The value of λ is λ=h/2mc=1.213 �? 10�??12 meters. The free electron radius is: r�??=1.213�?10�??12÷2�?=1.929 �? 10�??13 meters. Therefore, λd=2�?rd, a0=rd=274r�??=274 �? 1.929 �? 10�??13 meters= 5.2917721092 �? 10�??11 meters and the calculated results are consistent with the Bohr radius values.

From the above introduction, it can be seen that both free electrons and electrons in hydrogen atoms are circular and it can be said that electrons move in one plane. The extension of the range of electron motion in hydrogen atoms to three-dimensional space was chosen without understanding the electronic structure and basic assumption 2. It seems to be an incorrect behavior now (The idea that the movement of electrons outside the nucleus is random and elusive is the result of this hasty choice). The correct choice is to extend equation (23) to two-dimensional space and use it to calculate some physical quantities of hydrogen atoms. The method is to change,

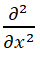
in equation (23) to �??2 and then let Z=0, in order to solve the Schrödinger equation under the condition of x2+y2=rd2. Previously, it was believed that the wave function of electrons in the s-shell of hydrogen atoms was spherically symmetric, with an angular quantum number Ld=0, resulting in a zero orbital magnetic moment. Now it seems that this is also incorrect. We believe that the motion of bound electrons outside the nucleus is an enhanced motion (a combination motion) of the spin motion of free electrons. Spin angular momentum is also a result of this combined motion. When the ring-shaped entity of electrons moves around an atom, an equilibrium state can be reached. The equilibrium state equation is

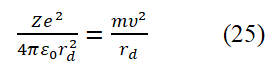
It is not difficult to see that, localized realism still holds a high position in such quantum mechanical systems.

Establish Dirac equation based on basic assumptions 1 and 2 (electronic structure model and hydrogen atom model)

We can also derive Klein Gordon equation and Dirac equation based on the electronic structure model of the photojunction [1]. The first derivative of Eq. (2)

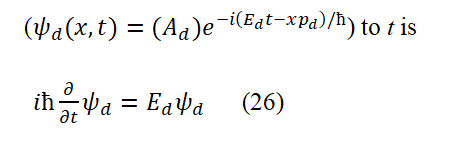
Taking hydrogen atom as an example, the total energy of electrons outside the nucleus is

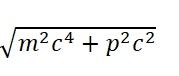
According to Eq. (26), we know

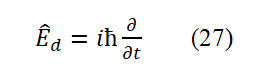
This is the total energy operator of the particles.

The total energy Ed of the electrons outside the hydrogen nucleus is: (the orbital kinetic energy of the electron T)+(potential energy V)+(the electron�??s intrinsic energy mc²):

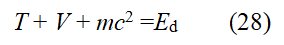
Here, md is m the mass of an electron (me). T=m�?2/2=αcpd/2, V=�??2T= �??m�?²=�??αcpd, T+V=�??(1/2)αcpd. The Virial theorem is a dynamic theorem for classical multi-particle equilibrium systems. Nor can relativistic effects destroy it. In Bohr's model of the hydrogen atom, it certainly holds. The virial theorem also holds for Saturn-like ring hydrogen atoms under hypothesis 2. Existing quantum mechanics also uses the virial theorem. Comparing the virial theorem 2T+V=0, pd=m�?d and �?d=αc (where Z=1) and Eq. (28) �??derived from the equilibrium Eq. (25) of classical mechanics�?�, we can get:

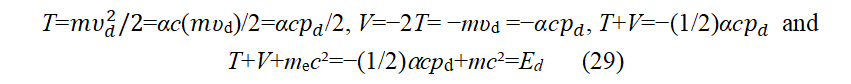
The relationship between the kinetic energy of a moving particle and the relativistic energy is mc ²Ã¯Â¿Â½??mc ²= T=(1/ αcp d. Using this formula to eliminate mc ² in Eq. (29), we have (Below, some footmarks will be omitted wit hout causing misunderstandings). In the following descr iption, we omi t the subscript d.

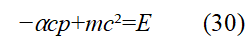
Eq. (30) can express that the total energy of the moving particle minus the kinetic energy of the particle equals the interna internal energy of the particle. Replace p and E in Eq. (30) with applying the operators expressed by Eqs. (9) and (20 ) to �?(x,t), respectively. Result in

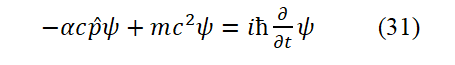
Eq. (31) is the Dirac equation. The meaning of the Dirac equation derived in this paper is that in the electrodynamics’ equilibrium system of hydrogen atom, the total energy of electrons in the system is equal to the sum of its relativistic tota total energy an d its potential energy. If the description is the motion of negative energy particles, the signs of the terms in the formula should be changed. Only by changing the sign of the mass alone can you get the exact same form as the Dirac equation. However, nega tive mass is caused by people mistakenly treating antiparticles as particles of negative energy (or negative mass). The α in the Eq. (31) is a specific constant constant—the fine structure constant and ⍺c is the fitted classical motion velocity of the electron outs ide the ground state hydrogen atom. However, before this article, α is not a simple constant (if certain conditions are met, α can take ± 1). The matrix form of α is not derived from Dirac, but written to satisfy the covariance of the Dirac equation under the Lorentz transformation. From this point of view, we cannot judge the correctness of the Dirac equation derived in this paper based on the original Dirac equation. It can be seen that it is not easy to deny the meaning of α given in this article. Only b y solving a number of Dirac equations specifically, and seeing whether the results are consistent with the facts. Eq. (31) must correspond to the energy summation Eq. (28)-(30), otherwise it is wrong. If α is not a fine structure constant, the energy on th e left side of the equations (30)-(33) is much greater than the energy on the right side [7].

If it is an ns electron outside the atomic core with an effective charge of Z Z*, the Dirac equation for a groundground-state hydrogen atom is

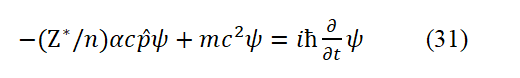
The original Dirac original equati on corresponding to Eq. (31) is

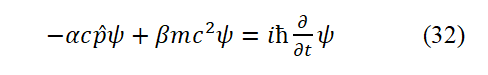
In the Eq. (32), β=± 1. α=± 1. When both α and β are takeen as −1, Eq. (32) becomes Eq. (

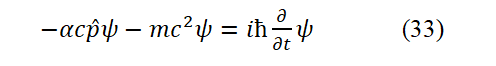
The energy signs on both sides of the equal sign of Eq. (33) are inconsistent, which is wrong. The reasons will be stated later. The problem of Eq. (32) is also the problem of Eq. (33). Since ψ in these two equations is defined by Eq. (1), so, Eqs. (31) an d (32) where

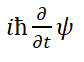
is the internal energy of the particle. As we all know, the relativistic total energy of a moving electron is

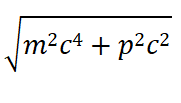
The absolute value of both sides of the equal ity sign of Eqs. (32) and (33) cannot be greater than it. It is equal to

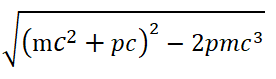
But less than ( mc ²+ pc ). If both α and β take +1, then the left side of Eq. (32) is greater than the right side (the equation does not hold). Under the premise that both α and β are taken as −1, even if the negative energy particle is described by equation (32), the equation does not hold. The system energy summation method corresponding to equation (32) is cp +mc ²= E. This is inconsistent with the correct energy expression (31), and is also incompatible with the Bohr hydrogen atomic model. The first term ( αcp ψ) on the left side of the original D irac Eq. (31) is the result of being erroneously enlarged by a factor of 137 by Dirac. On the premise that α=± 1 is admitted, no matter whether the signs of α and β are the same or opposite, Eq. (31) is wrong.

Compared with the original Dirac equation expr essed b y Eq. (32), the Dirac equation (Eq. (33)) derived in this paper has at least 3 advantages: First, the meaning of α is clear; Second, the equation is more in line with the energy summation method; Third, the Eq. (29) is derived, whereas Dirac wrote h is equations purely by intuition.

Taking the second second-order partial derivative of Eq. (2) with respect to t and compari ng it with Eq. (25), we can get

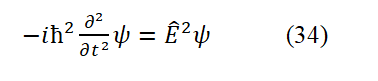
The total relativistic energy applicable to the ov erall motion of the particle is

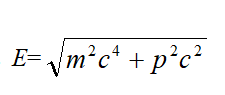
Square both sides of the equation, divide the terms by c ² and shift the terms to get

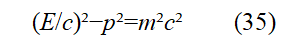
Representing E² and p ²in Eq. (34) by Eq. (33) and Eq. (17), respectively, Result in

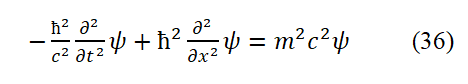
Eq. (35) is Klein Klein-Gordon’s equation. Here ψ is the wave equation for plane polarized light. Eq. (35) corresponds to the expression of the relative momentum squared ( E/c )2=m2c2+p2.

de Broglie waves ( i.e., beat waves in hypothesis 2), are also fitted matter waves. The frequency of this fitted wave is 1/274 of the frequency of the elementary photon. h hνd is the kinetic energy T of the composite wave (where νd is the frequency of the fitted matter wave, that is, the frequency of the de Broglie wave). The fitted velocity (apparent velocity) of the fitted matter wave is υ= ⍺c. This velocity was formerly known as the group velocity of de Broglie wave. The relationship between the energy and momentum of the fitted matter wave is also a classical mechanical relationship: T=p υ/2= 2=⍺cp/2. Since the classical motion is fitted, the calculation method used must include the classical mechanics method. In this case, h hν= E in Eq. (10) is the kinetic energy of the particle Ek=T. Meanwhile, we have

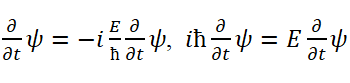
Comparing Eq. (19) with Eq. (27), considering Ek=T, and T+V=E, the time time-dependent Schrödinger equation can be obtai obtained.

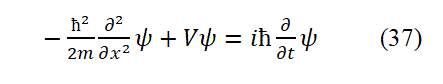
Simultaneously calculating hydrogen molecules based on the material structure model of localized realism and wave dynamics

Quantum chemists need to know the potential energy function of the system when calculating molecules and atoms. However, due to the unknown motion state of electrons, the form of the potential energy function for the interaction between at least paired electrons is unknown. Even if some are known, the interaction energy between electrons cannot be accurately calculated due to their uncertain positions. They had to subjectively and tentatively establish a potential energy function. This makes quantum chemistry methods belong to semi empirical methods. Removing the hat of semi empirical methods and easily calculating data for some molecules must be the dream of quantum chemists.

By using pure mathematical methods to extend equation (23) to three-dimensional situations, we can obtain

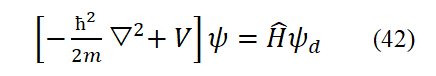
For hydrogen atoms, this "generalization" operation is equivalent to acknowledging that the motion of electrons outside the nucleus is not a simple motion in the classical sense. It has been explained above that equation (23) can also be derived from the electronic structure model of the photojunction. Simply put, the electronic structure model of the photonic junction does not exclude existing quantum mechanical calculation methods (as long as the potential energy function can be given, atoms and molecules can greatly simplify the calculation process by using hydrogen like atoms). Just modify the concept of "probability density" to "energy density".

The three assumptions in this article are not independent, but interconnected. Specifically, they all revolve around the same core. The core is that the simplest circularly polarized photons propagate end-to-end along a circle, forming a fundamental particle with localized energy and constant charge [8]. This type of electron has three major characteristics: Composition—the simplest circularly polarized photon; structure—wave rings connected at the beginning and end; important feature-in a potential field, a wave can be extended into a beat wave according to Huygens' principle.

The main energy level of the 1s² electron in helium atoms should be the same, so the ionization energy should be the same. The difference in ionization energy between these two electrons is the pairing energy of 1s² electrons in helium atoms. The reason is that without the influence of another electron, the ionization energy of these two electrons is the same at 1s². The difference in ionization energy between them is the result of the interaction between these two electrons. The difference in ionization energy of 1s² electrons of each atom can be found in the chemistry manual. According to the ionization energy data of elements, the regression analysis method can be used to obtain the regression equation (43) between the 1s2 electron pairing energy and the effective nuclear charge number [8].

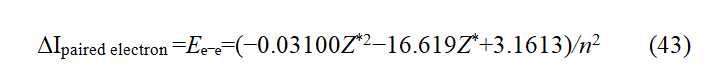
The unit of energy in equation (43) is electron volts. The regression equations calculated using different amounts of ionization energy data and software may vary slightly (readers with conditions should choose better statistical tools). Equation (43) shows that when the effective charge is zero, the energy released when free electrons pair is 3.1613 eV. This is the pairing energy Δ of free electrons.

According to assumptions 1, 2, and 3 in this article, it can be inferred that a hydrogen molecular ion is an electron sphere in an electrokinetic equilibrium system between two hydrogen nuclei (Figure 1).

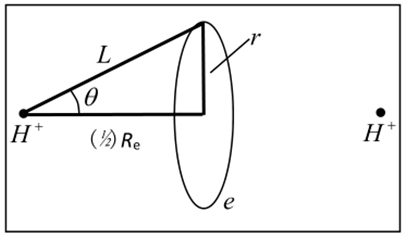
Figure 1. Hydrogen molecule-ion H�??+.

Discussion

The ground state hydrogen molecule is a charged ring with a pair of electrons overlapping between two hydrogen nuclei. This structure can achieve classical electrodynamic equilibrium and is a locally recognized microstructural system. It is inevitable to be able to use classical electrodynamics methods (or Bohr planetary models) for calculations. In this case, hydrogen molecules and helium atoms are extremely similar in composition and structure. The only difference between the two is that the two protons in a hydrogen molecule are separated, while the two protons in a helium atom are bound together. Classical electrodynamics and wave dynamics methods of planetary models can be used simultaneously. The planetary model of helium atoms involves two paired electrons rotating around a helium nucleus. The wave mechanics description of helium atoms is the Schr ö dinger equation description of two hydrogen like atoms. The author's calculation results show that the dissociation energy and bond length are D�??=−4.2 eV, and the bond length R�??≈ 0.71 × 10–10 m [9]. The relative experimental values are: D�??=−4.75eV, R�??=0.74 × 10–10 m. The error is related to the failure to consider the magnetic moment interaction between nuclei. The calculation results of hydrogen molecular ions in reference [4] are as follows: D�??=−6.2eV�?R�??≈ 1.1 × 10–10 m. The corresponding experimental value is D�??=−2.8 eV�?R�??≈ 1.06 × 10–10 m. For hydrogen molecular ions, there is a large error in the calculation of dissociation energy. The reason is that hydrogen molecular ions only have one electron, and the interaction between their orbital magnetic moment and nuclear magnetic moment is asymmetric, resulting in molecular asymmetry and significant errors.

This is the first data on hydrogen molecules calculated by humans using classical structures and wave dynamics. Although empirical formulas were used to calculate the electronic pairing energy during the calculation process, this empirical formula is a universal formula and is derived from experimental experiments (the calculation results for different situations remain unchanged). This is much more objective than the previous subjective method of providing empirical potential energy functions. The calculation method is based on local realism. This indicates that classical electrodynamics methods are compatible with wave dynamics methods. From Figure 1, it can be intuitively seen that the quantum chemistry calculation method provided in this article is a local realism approach [9].

The same method can be used to calculate the lithium molecule Li2. Unlike hydrogen molecules, the bonding electrons of lithium molecules are at the n=2 energy level. The calculation result is: dissociation energy The calculation result is: dissociation energy D�??=−1.19 eV, bond length R�??≈ 2.56 × 10-10 m. The corresponding experimental value is D�??=−1.06 eV, and the bond length R�??≈ 2.67 × 10–10 m. The error is also related to the nuclear magnetic interaction between the two nuclei.

The planetary atomic model is applied to atoms other than hydrogen and atomic reality

The planetary atomic model of atoms is an extended concept. Under the framework of the photojunction electron model, changing the planetary model to the Saturn model concept is more appropriate. In fact, the Saturn model of atoms is a fitted model that conforms to the laws of classical physics. The reason is that the quasi satellite rings in atoms are not solid rings, but wave rings, but overall, the mass equivalent to the energy of the ring wave is indeed distributed on the ring electrons In this way, there are no stability and quantization difficulties. Due to the high compatibility between the Saturn model of atoms and the wave dynamics model, we can simultaneously use the wave dynamics method and the classical electrodynamics method under the Saturn model to calculate the energy of atoms. In other words, we can add a planetary model calculation scheme for all atoms.

From sections 1-9, readers can see that the application results of this section are inevitable. These are also some successful application examples of localized realism quantum mechanics.

Conclusion

The author has completed the following list of 10 scientific events that occurred for the first time in human society. That is to say, the following ten groundbreaking works have been completed for the first time in the history of technology to fill the world gap. The occurrence of the following 10 scientific events is based on revealing the internal composition, structure and motion forms of electrons.

A complete electronic structure model of optical junction is established (a new scheme of electronic internalcomposition, structure and movement is proposed and hundreds of application examples are provided).

The electron radius is calculated by classical structure, classical rotation and classical electromagnetism.

The electron spin angular momentum and the electron spin magnetic moment, as well as the electron spin angularmomentum operator and the electron spin magnetic moment operator, are calculated by using the classicalstructure and the classical mechanical method.

Using classical structure, classical rotation and classical mechanics methods, the electronic orbital angularmomentum of hydrogen atom is calculated (note: it was previously thought that electrons in hydrogen atom have noorbital motion).

The electronic orbital magnetic moment of hydrogen atom and its operator are calculated by classical structure andclassical mechanical method (note: it was previously thought that the electrons in hydrogen atom have no orbitalmotion).

Using classical structure and classical mechanics method, the experimental measurement method of electronpairing energy-the difference of ionization energy of two paired electrons is obtained.

The theoretical basis of the compatibility between the planetary model or Saturn model method and the quantummechanics method is established and a large number of examples of the mixed use of these two methods aregiven.

The bond length and dissociation energy of hydrogen molecule and hydrogen molecule ion are calculated byclassical structure and classical mechanical method.

The mathematical formal system of quantum mechanics is established by using the internal composition, structureand intrinsic motion form of electrons, as well as classical mechanical laws (for example, classical momentum-velocity relationship p=mυ, classical kinetic energy-momentum relationship Ek=p²/2m, planetary motion equationunder electrodynamics, angular momentum expression and electric potential energy expression f(r, Z, e,etc.) of planetary equilibrium system. This lays a theoretical foundation for the compatibility and even equivalencebetween quantum mechanical methods and classical mechanical methods under the background of Bohr planetarymodel.

The specific form of electron spin function, the angular momentum operator of electron orbital motion, the magneticmoment operator of electron orbital motion and the specific meaning of α in Dirac equation-fine structure constantare given by using the internal composition, structure and intrinsic motion state of electrons.

References

1. Srednicki M. Quantum field theory. Cambridge University Press; 2007.

   [Google Scholar]

2. Weinberg S, et al. Quantum Field Theory. World Book Publishing Company. 2014; 2.
3. Tu R, et al. Progress and review of applied research on new theory of electronic composition and structure. Infinite Energy. 2024;28.
4. Runsheng Tu, et al. Quantum mechanics�?? reurn to local realism, Cambridge Scholars Press. 2015.
5. Tu R, et al. Some success applications for local-realism quantum mechanics: Nature of covalent-bond revealed and quantitative analysis of mechanical equilibrium for several molecules. J Modern Phys. 2014;5:10.

   [Google Scholar]

6. Tu R, et al. The principle and application of experimental method for measuring the interaction energy between electrons in atom. Int J Sci Rep. 2016;2:187-200.

   [Crossref]

7. Jingyou T, et al. Atomic physics and quantum mechanics. Peking University Press. 2011.
8. Feynman R, et al. Today's physics. Beijing, Science Press, Beijing, China. 1981:168-173.
9. Kedia H, et al. Tying knots in light fields. Phys Rev Lett. 2013;111:150404.

   [Crossref] [Google Scholar] [PubMed]