ISSN: 2322-0066
ISSN: 2322-0066
Samuel Bonaya Buya*
Mathematics/Physics teacher at Ngao girls, Secondary School, Kenya
Received date: 15/06/2017; Accepted date: 10/10/2017; Published date: 13/10/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
This research includes a method of solving the Septic equation by expansion. The aim of this research is to contribute further to the knowledge of Septic equations. The Method can be used as a standard basis for deriving formulae for polynomial equations of degree three and above
Polynomial equations, Septic equation, Cubic equation
The objective of this paper is to add further to the research into the solution quintic of equations that has preoccupied mathematicians for centuries.
Quintic equations are part of polynomial equations. From literature [1,2] polynomial equations were first investigated more than four thousand years ago.
The general septic equation takes the form 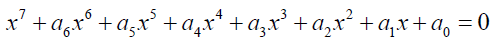 (1)
(1)
Abel and Ruffini showed that proved that it impossible to solve over a field of rational numbers [3].
In this paper I will present a solution of the septic equation:
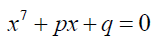 (2)
(2)
In the process of deriving the Septic equation above, there will also be need to solve a Quartic equation with the formula of the quartic equation derived without reducing it to a lower form. This will imply that formulae of higher degree polynomials can be derived without eliminating the intermediate terms [4].
In the above septic equation four intermediate terms have been eliminated. I will attempt to derive its formula with a method that can be also used to derive the general septic equation [5,6].
The advantage of this method is that it can be used to derive formulae for polynomial equations of degree three and above.
Solution of the cubic equation
Consider the cubic equation,
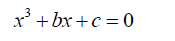 (3)
(3)
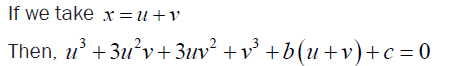 (4)
(4)
The expanded form of 4 is:
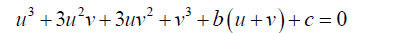 (5)
(5)
5 can be simplified to take the form:
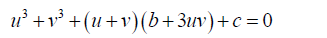 (6)
(6)
Take 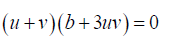 (7)
(7)
And 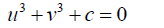 (8)
(8)
From 7 b = 3uv
Substituting 8 into 9 and simplifying:
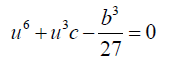 (10)
(10)
One of the roots of 10 is
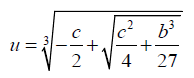 (11)
(11)
Similarly it can be shown that one of the roots of v is given by:
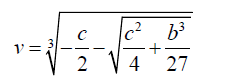 (12)
(12)
One root of the above cubic equation is given by,
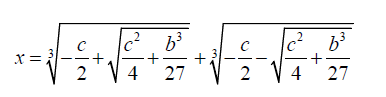 (13)
(13)
The above method can be extended to provide a solution to the Septic equation.
Solution of the Septic equation
Consider the Septic equation below
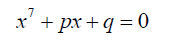 (14)
(14)
If we take x = u + v then,
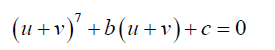 (15)
(15)
The expanded form of 15 is:
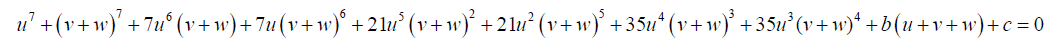 (16)
(16)
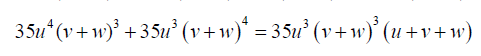 (17)
(17)
Substituting 17 into 16
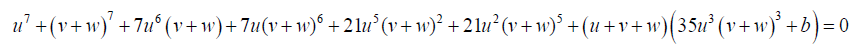
Take:
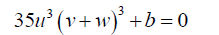 (18)
(18)
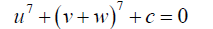 (19)
(19)
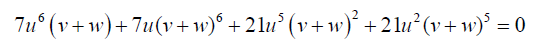 (20)
(20)
Equation 20 can be simplified to:
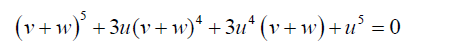 (21)
(21)
Substituting 18 into 19,
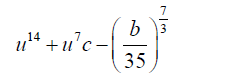 (22)
(22)
One of the roots of 21 is given by:
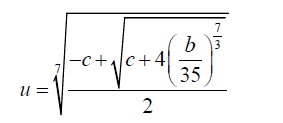 (23)
(23)
In solving the quintic equation 21 above:
Take 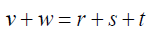 (24)
(24)
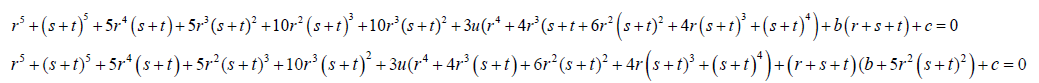 (25)
(25)
Equations:
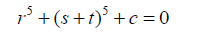 (26)
(26)
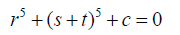 (27)
(27)
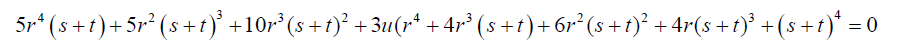 (28)
(28)
Substituting 26 into 27:;
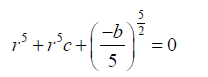 (29)
(29)
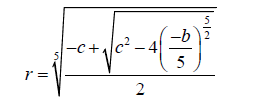 (30)
(30)
Equation 1.7 can be reorganized as:
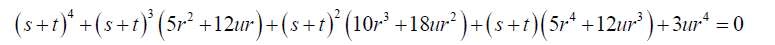 (31)
(31)
Let s + t =W
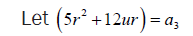 (32)
(32)
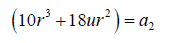 (33)
(33)
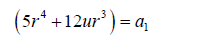 (34)
(34)
3ur4=a0
Then:
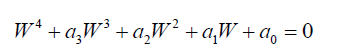 (36)
(36)
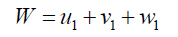 (37)
(37)
Then:
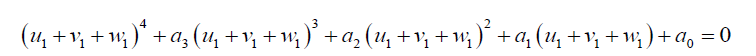 (38)
(38)
Then:
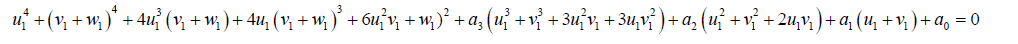 (39)
(39)
But 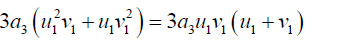 (40)
(40)
Equation 39 can be simplified to:
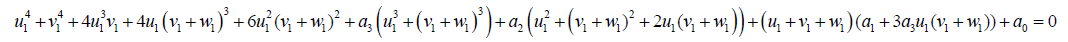 (41)
(41)
Equations from 41:
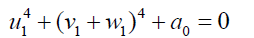 (42)
(42)
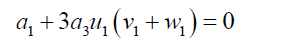 (43)
(43)
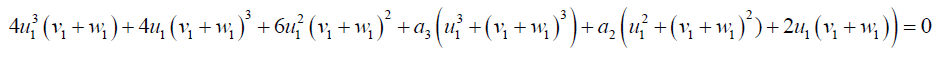 (44)
(44)
Substituting 43 into 42 and simplifying:
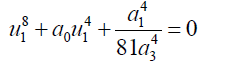 (45)
(45)
One of the roots of 45 is given by:
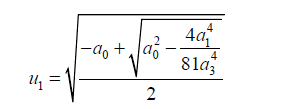 (46)
(46)
Simplifying and rearranging 44:
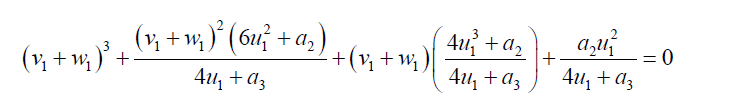 (47)
(47)
If
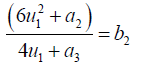 (48)
(48)
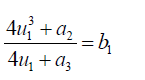 (49)
(49)
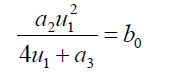 (50)
(50)
Then 47 can be written as:
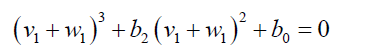 (51)
(51)
If we take
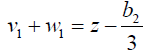 (52)
(52)
Then: 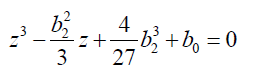 (53)
(53)
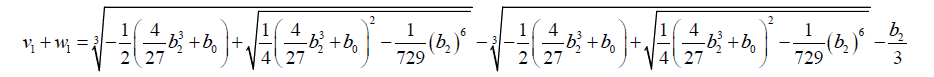 (54)
(54)
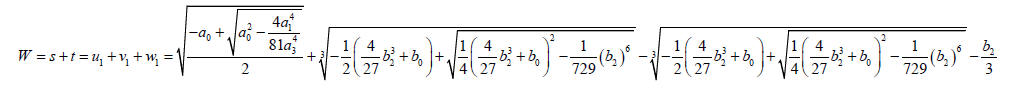 (55)
(55)
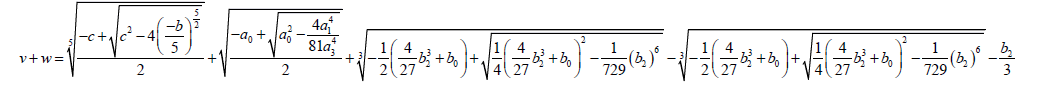 (56)
(56)
One of the roots of the septic equation is given by:
x = u + v + w
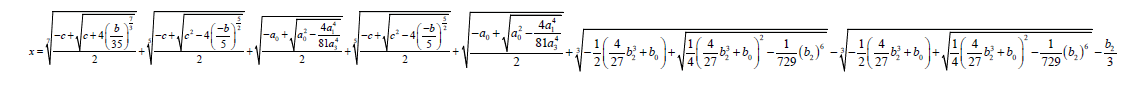 (57)
(57)
I would like to express my since gratitude to the following:
The Almighty God for making this piece of work successful, my wife for her Julie Ahadi encouragement and service.